02-데이터 – Nextra

1. 0과 1로 숫자를 표현하는 방법

컴퓨터는 0과 1로 모든 정보를 표현하고, 0과 1로 표현된 정보만을 이해할 수 있습니다.

그러면 3+4는 어떻게 계산될까?
또 컴퓨터는 숫자 3과 4를 어떻게 인식할까?

1.1 정보 단위

1.1.1 비트

비트(bit) : 0과 1을 나타내는 가장 작은 정보 단위
e.g. 비트는 전구에 빗대어 생각해 보면 이해하기 쉬움
- 전구 한 개로 (꺼짐) 혹은 (켜짐), 2가지 상태를 표현할 수 있듯,
- 1 비트는 0 또는 1, 두 가지 정보를 표현 가능

MySelf-Architec-Oper_2_1

두 개의 전구
- (꺼짐, 꺼짐), (꺼짐, 켜짐), (켜짐, 꺼짐), (켜짐, 켜짐), 4가지 상태를 표현
- 따라서 2비트는 4가지 정보를 표현
세 개의 전구
- 8가지 상태를 표현할 수 있습니다.
- 따라서 3비트는 8가지 정보를 표현

n개의 전구로 표현할 수 있는 상태는 $2^n$ 가지입니다. 같은 개념으로 n비트는 $2^n$ 가지 정보를 표현할 수 있습니다.

1.1.2 다른 단위

웹 브라우저, 워드 프로세서, 포토샵 등 모든 프로그램은 수십만, 수백만 개 이상의 0과 1로 이루어져 있습니다. 즉, 우리가 실행하는 프로그램은 수십만 비트, 수백만 비트로 이루어져 있죠.

그런데 우리가 일상적으로 프로그램의 크기를 말할 때는 표현의 편의를 위해 비트보다 큰 단위를 사용합니다.

1 바이트(byte) : 여덟 개의 비트를 묶은 단위로, 비트보다 한 단계 큰 단위
- 하나의 바이트가 표현할 수 있는 정보는 몇 개일까요?
- 1바이트는 8비트와 같으니 $2^8$ (256)개의 정보를 표현 가능
1킬로바이트(kB; kilobyte) : 1바이트 1,000개를 묶은 단위
1메가바이트(MB; megabyte) : 킬로바이트 1,000개를 묶은 단위
1기가바이트(GB; gigabyte) : 1메가바이트 1,000개를 묶은 단위를
1테라바이트(TB; terabyte) : 1기가바이트 1,000개를 묶은 단위
- 테라바이트보다 더 큰 단위도 있으나 보통 다루게 될 데이터의 크기는 최대 테라바이트까지인 경우가 많음

단위	크기
1바이트	8 비트(8 bit)
1킬로바이트	1,000 바이트 (1,000 byte)
1메가바이트	1,000 킬로바이트(1,000 KB)
1기가바이트	1,000 메가바이트(1,000 MB)
1테라바이트	1,000 기가바이트 (1,000 GB)

💡 참고

1kB는 1,024byte, 1MB는 1,024kB… 이런 식으로 표현하는 것은 잘못된 관습입니다. 이전 단위를 1,024개 묶어 표현한 단위는 kB, MB, GB, TB가 아닌 KiB, MiB, GiB, TiB입니다.

💡 워드(word)

워드 : CPU가 한 번에 처리할 수 있는 데이터 크기

CPU가

한 번에 16비트를 처리할 수 있다면 1워드는 16비트가 되고,

한 번에 32비트를 처리할 수 있다면 1워드는 32비트가 됨

워드의 크기에 따라

하프 워드(half word) : 정의된 워드의 절반 크기

풀 워드(full word) : 정의된 워드의 1배 크기

더블 워드(double word) : 정의된 워드의 2베 크기

워드 크기가 큰 CPU는 한 번에 처리할 수 있는 데이터가 큼

워드 크기는 CPU마다 다르지만, 현대 컴퓨터의 워드 크기는 대부분 32비트 또는 64비트입니다.

e.g. 가령 인텔의 x86 CPU는 32비트 워드 CPU, x64 CPU 는 64비트 워드 CPU입니다.

1.2 2진법

수학에서 0과 1만으로 모든 숫자를 표현하는 방법을 2진법(binary)이라고 합니다. 2진법을 이용하면 1보다 큰 수도 0과 1만으로 표현할 수 있습니다. 바로 숫자가 1을 넘어가는 시점에 자리 올림을 하면 됩니다.

사람은 숫자를 셀 때 9를 넘어가는 시점에 자리 올림을 합니다 9 다음이 10 처럼요. 이는 우리가 10진법(decimal)을 사용하기 때문입니다. 10진법은 숫자가 9를 넘어가는 시점에 자리 올림을 하여 0부터 9까지, 열 개의 숫자만으로 모든 수를 표현하는 방법입니다.

이와 유사하게 2진법은 숫자가 1을 넘어가는 시점에 자리 올림을 하여 2개의 숫자만으로 모든 수를 표현합니다.

MySelf-Architec-Oper_2_2

가령, 10진수 2를 컴퓨터에 알려주려면?

2 (10진수)
10 (2진수, ‘일영’)

10진수 8을 컴퓨터에 알려 주려면?

8 (10진수)
1000 (2진수, ‘일영영영’)

그런데 여기서 문제가 있습니다. 숫자 10만 보고 이게 10진수인지 2진수인지 구분이 안됩니다. 숫자 10을 10진수로 읽으면 10이지만, 2진수로 읽으면 2입니다. 이처럼 숫자만으로는 어떤 진법으로 표현된 수인지 알 수 없습니다.

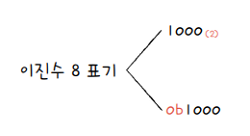
MySelf-Architec-Oper_2_3

이런 혼동을 예방하기 위해 2진수 끝에 아래첨자를 붙이거나, 2진수 앞에 0b를 붙입니다. 전자는 주로 2진수를 수학적으로 표기할 때, 후자는 주로 코드 상에서 2진수를 표기할 때 사용합니다.

10진법	2진법
10진법으로 표현한 수	2진법으로 표현한 수
사람이 사용하는 숫자 표현법	컴퓨터가 사용하는 숫자 표현법
	수학에서는 `아래첨자로 (2)`
	코드상에서는 `ob`

1.2.1 2진수의 음수 표현

사람이 쓰는 10진수는 음수를 표현할 땐, -1, -3, -5 같이 단순히 숫자 앞에 마이너스 부호를 붙임

컴퓨터는 0과 1만 이해할 수 있기 때문에, 마이너스 부호를 사용하지 않고 0과 1만으로 음수를 표현해야 합니다.

MySelf-Architec-Oper_2_4

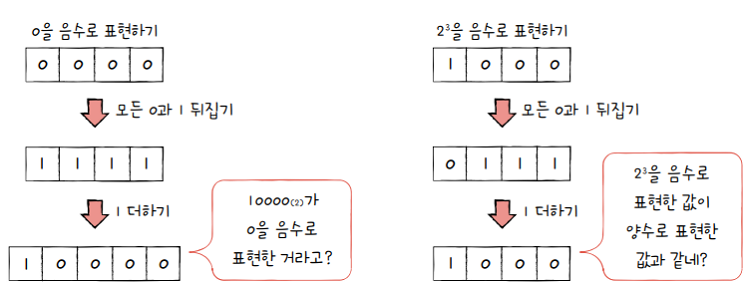
2의 보수(two’s complement)
- 0과 1만으로 음수를 표현하는 방법 중 가장 널리 사용되는 방법
- 2의 보수를 구해 이 값을 음수로 간주하는 방법
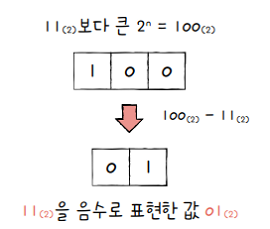
- 사전적 의미는 “어떤 수를 그보다 큰 $2^n$ 에서 뺀 값“을 의미
- e.g. 0b11의 2의 보수는
  - 0b11보다 큰 $2^n$
  - 즉, 0b100에서 0b11을 뺀 0b01이 됨

하지만 굳이 이렇게 사전적 의미로 어렵게 이해할 필요는 없습니다.

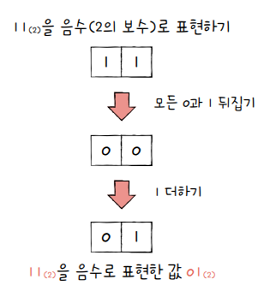
MySelf-Architec-Oper_2_5

2의 보수를 매우 쉽게 표현하면
- 모든 0과 1을 뒤집고, 거기에 1을 더한 값
- e.g. 0b11의 모든 0과 1을 뒤집으면 Ob00이고,
- 거기에 1을 더한 값은 0b01입니다. 즉, 0b11의 **2의 보수(음수 표현)**는 0b01

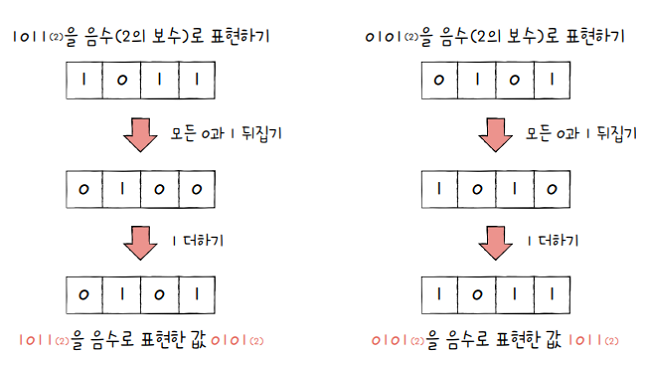
MySelf-Architec-Oper_2_6

0b1011의 음수를 구해봅시다.

1011에서 모든 0과 1을 뒤집으면 0100이고, 여기에 1을 더한 값은 0101
- 즉, 0101은 1011의 음수입니다.
정말 이 값이 1011의 음수인지 확인하려면?
- 어떤 수의 음수를 두 번 구하면 처음의 그 수가 됩니다.
  - e.g. -(-A) = A인 것처럼요. 2의 보수도 마찬가지입니다.
- 어떤 수의 2의 보수를 두 번 구해보면 자기 자신이 됩니다.
- 마찬가지로 1011의 2의 보수를 두 번 구해 보면 자기 자신인 1011이 됩니다.

그러면,

-1011을 표현하기 위한 음수으로서의 0101과 10진수 5를 표현하기 위한 양수로서의 0101은 똑같이 생겼는데,
2진수만 보고 이게 음수인지 양수인지 어떻게 구분할까요?
실제로 2진수만 봐서는 이게 음수인지 양수인지 구분하기 어렵습니다.
그래서 컴퓨터 내부에서 어떤 수를 다룰 때는 양수인지 음수인지를 구분하기 위해 플래그(flag)를 사용합니다.
- 플래그는 쉽게 말해 부가 정보
- 컴퓨터 내부에서 어떤 값을 다룰 때 부가 정보가 필요한 경우 플래그를 사용

플래그는 04장에서 자세히 다루니 지금은

컴퓨터 내부에서 숫자들은 ‘양수’ 혹은 ‘음수’가 적혀 있는 표시를 들고 다니므로
컴퓨터가 부호를 헷갈릴 일은 없다 정도로만 생각해도 무방합니다.

💡 2의 보수 표현의 한계

2진법 음수를 표현하기 위해 2의 보수를 취하는 방식은 아직까지도 가장 널리 사용되는 방식이지만, 완벽한 방식은 아닙니다.

0이나 $2^n$ 형태의 2진수에 2의 보수를 취하면, 원하는 음수값을 얻을 수 없습니다.

첫 번째 경우 자리 올림이 발생한 비트의 1을 버립니다.

하지만 두 번째 경우와 같이 $2^n$ 의 보수를 취하면

자기 자신이 되어 버리는 문제는 본질적으로 해결하기 어렵습니다.

즉, n비트로는 - $2^n$ 과 $2^n$ 이라는 수를 동시에 표현할 수 없습니다.

1.3 16진법

2진법을 이용하면 컴퓨터가 이해하는 숫자 정보를 직접적으로 표현할 수 있습니다. 하지만 0과 1만으로 모든 숫자를 표현하다 보니 숫자의 길이가 너무 길어진다는 단점이 있습니다. 10진수 32를 10진수로 표현하면 0b100000과 같이 6개의 자릿수가 필요한 것처럼요. 그래서 데이터를 표현할 때 2진법 이외에 16진법도 자주 사용합니다.

MySelf-Architec-Oper_2_8

16진법(hexadecimal) : 수가 15를 넘어가는 시점에 자리 올림을 하는 숫자 표현 방식
- 십진수 10, 11, 12, 13, 14, 15를 16진법 체계에서는 각각 A, B, C, D, E, F로 표기
- 2진수에 비해 더 적은 자릿수로 더 많은 정보를 표현할 수 있겠죠?

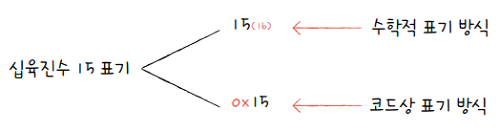
MySelf-Architec-Oper_2_9

16진수도 2진수와 마찬가지로 숫자 뒤에 아래첨자 (16)를 붙이거나, 숫자 앞에 0x를 붙여 구분합니다. 전자는 주로 수학적으로 16진수를 표기할 때, 후자는 주로 코드상에서 16진수를 표기할 때 사용되는 방식입니다.

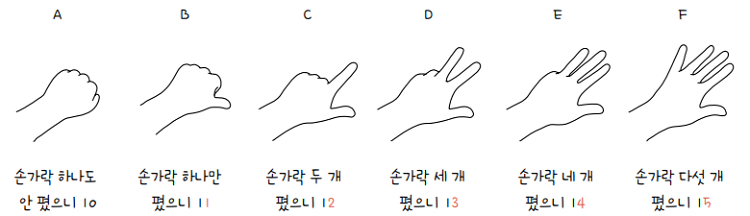
💡 16진수A~F를 쉽게 이해하는 방법

16진법을 처음 접했다면 16진수A가 10, 16진수B가 11을 뜻한다는 사실이 잘 와닿지 않을 겁니다. 그림처럼 손가락으로 직접 꼽아 보면 이해하기 편합니다.

‘주먹을 쥐었을 때가 A’라고 생각해 보세요. 손가락을 하나도 안 폈으니 0입니다.

16진수D는 십진수로 무엇일까요?

주먹을 쥐었을 때가 A라고 했으니 A, B, C, D 차례로 손가락을 하나씩 펴면

D는 손가락이 세 개 펴집니다.

따라서 16진수 D는 13입니다.

그런데 왜 굳이 16진법을 사용할까요? 우리가 편하게 쓰는 십진법도 있는데 말이죠. 여러 가지 이유가 있지만, 16진법을 사용하는 주된 이유 중 하나는 2진수를 16진수로, 16진수를 2진수로 변환하기 쉽기 때문입니다.

1.3.1 16진수를 2진수로 변환

16진수는 한 글자당 열여섯 종류(0~9, A~F)의 숫자를 표현할 수 있습니다. 그렇다면 16진수를 이루는 숫자 하나를 2진수로 표현하려면 몇 비트가 필요할까요? 4비트가 필요합니다. $2^4$ = 16이니까요.

16진수를 2진수로 변환하는 간편한 방법 중 하나는 16진수 한 글자를 4비트의 2진수로 간주하는 겁니다.

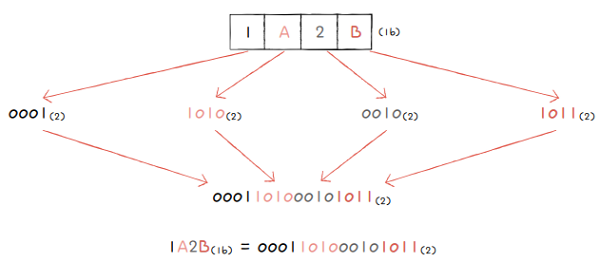
MySelf-Architec-Oper_2_11

즉, 16진수를 이루고 있는 각 글자를 따로따로 (4개의 숫자로 구성된) 2진수로 변환하고,
그것들을 그대로 이어 붙이면 16진수가 2진수로 변환됩니다.
예를 들어, $1A2B_{(16)}$ $1 A 2 B_{(16)}$ 라는 16진수가 있을 때,
- 각 숫자 $1_{(16)}, A_{(16)}, 2_{(16)}, B_{(16)}$ 를 2진수로 표현하면 0001, 1010, 0010, 1011입니다.
- 이 숫자를 그대로 이어 붙인 값, 즉 0001. 1010. 0010. 1011이 $1A2B_{(16)}$ 를 2진수로 표현한 값입니다.

1.3.2 2진수를 16진수로 변환

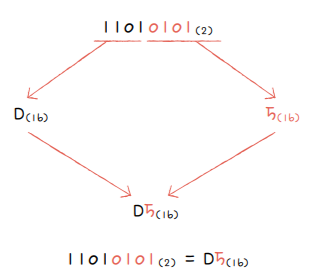
MySelf-Architec-Oper_2_12

2진수를 16진수로 변환할 때는

2진수 숫자를 네 개씩 끊고, 끊어준 4개의 숫자를 하나의 16진수로 변환한 뒤 그대로 이어붙이면 됩니다.
예를 들어, 1101. 0101이라는 2진수를 4개씩 끊으면 1101, 0101이고
이는 각각 $D_{(16)}$ 와 $5_{(16)}$ 이므로 이를 그대로 이어 붙인 $D5_{(16)}$ 가 11010101를 16진수로 변환한 수입니다.

2진수를 10진수로 변환할 때는 이렇게 간단하지 않기에 2진수를 16진수로 묶어 표현하는 것입니다.

💡 코드에 16진수를 직접 넣는 사례

16진수는 프로그래밍할 때 2진수와 더불어 자주 사용되므로 기억해두는 것이 좋습니다. 하드웨어와 밀접하게 맞닿아 있는 개발 분야에서는 코드에 16진수를 직접 쓰는 경우도 있습니다.
1offset = __mem_to_opcode_arm(*(u32 *)loc);
2offset = (offset & 0x00ffffff) << 2;
3if (offset & 0x02000000)
4offset -= 0x04000000;
5offset += sym->st_value - loc;

1.4 핵심포인트

비트는 0과 1로 표현할 수 있는 가장 작은 정보 단위입니다.
바이트, 킬로바이트, 메가바이트, 기가바이트, 테라바이트는 비트보다 더 큰 정보 단위입니다.
2진법은 1을 넘어가는 시점에 자리 올림을 하여 0과 1만으로 수를 표현하는 방법입니다.
2진법에서 음수는 2의 보수로 표현할 수 있습니다.
16진법은 15를 넘어가는 시점에 자리 올림하여 수를 표현하는 방법입니다.

1.5 확인 문제

Q1 2000MB는 몇 GB인가요?

Q2 다음 중 옳지 않은 것을 골라 보세요.

1000GB는 1TB와 같습니다.
1000kB는 1MB와 같습니다.
1000MB는 1GB와 같습니다.
1024bit는 1byte와 같습니다.

Q3 $1101_{(2)}$ 의 음수를 2의 보수 표현법으로 구해 보세요.

모든 0과 1 뒤집기
1 더하기

Q4 $DA_{(16)}$ 를 2진수로 표현하면 무엇인가요?

Q5 2진수와 더불어 16진수가 많이 사용되는 대표적인 이유는 무엇인가요?

2진수와 16진수 간의 변환이 쉽기 때문입니다.
16진수에 비해 2진수로 표현되는 글자 수가 일반적으로 적기 때문입니다.
16진수가 십진수보다 일상적으로 더 많이 사용되기 때문입니다.
컴퓨터는 2진수를 이해하지 못하기 때문입니다.

2. 0과 1로 문자를 표현하는 방법

컴퓨터는 키보드로 입력한 문자들을 실시간으로 모니터에 띄워 줍니다. 컴퓨터는 0과 1만 이해할 수 있다고 했는데, 입력한 문자를 어떻게 이해하고 모니터에 출력하는 걸까요?

2.1 문자 집합과 인코딩

0과 1로 문자를 표현하는 방법에 대해 알아보기 전에 여러분이 반드시 알아야 할 3가지 용어가 있습니다.

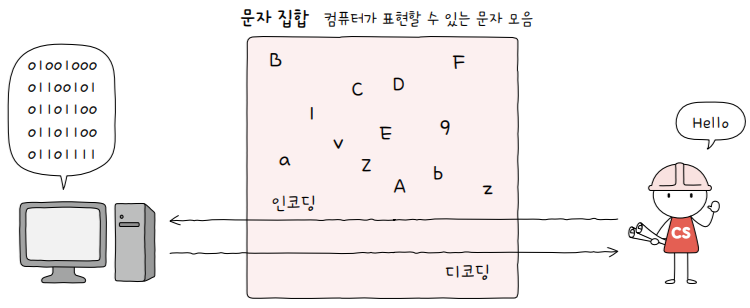
MySelf-Architec-Oper_2_13

문자 집합(character set)
- 컴퓨터가 인식하고 표현할 수 있는 문자의 모음
- 컴퓨터는 문자 집합에 속해 있는 문자를 이해할 수 있고,
- 반대로 문자 집합에 속해 있지 않은 문자는 이해할 수 없습니다.
- e.g. 문자 집합이 {a, b, c, d, e}인 경우 컴퓨터는 5개의 문자는 이해할 수 있고, f 나 g 같은 문자는 이해하지 못함
문자 인코딩(character encoding)
- 문자 집합에 속한 문자라고 해서 컴퓨터가 그대로 이해할 수 있는 건 아님
- 문자를 0과 1로 변환해야 비로소 컴퓨터가 이해
- 이 변환 과정을 문자 인코딩이라 하고 인코딩 후 0과 1로 이루어진 결과값이 문자 코드가 됨
- 같은 문자 집합에 대해서도 다양한 인코딩 방 법이 있음
문자 디코딩(character decoding)
- 인코딩의 반대 과정
- 즉, 0과 1로 이루어진 문자 코드를 사람이 이해할 수 있는 문자로 변환하는 과정

2.2 아스키 코드

아스키(ASCII; American Standard Code for Information Interchange)

초창기 문자 집합 중 하나로, 영어 알파벳과 아라비아 숫자, 그리고 일부 특수 문자를 포함합니다.
아스키 문자 집합에 속한 문자(이하 아스키 문자) 들은 각각 7비트로 표현되는데,
7비트로 표현할 수 있는 정보의 가짓수는 27개로, 총 128개의 문자를 표현할 수 있습니다.
실제로는 하나의 아스키 문자를 나타내기 위해 8비트(1바이트)를 사용합니다.
하지만 8비트 중 1비트는 패리티 비트(parity bit)라고 불리는, 오류 검출을 위해 사용되는 비트이기 때문에
실질적으로 문자 표현을 위해 사용되는 비트는 7비트입니다.

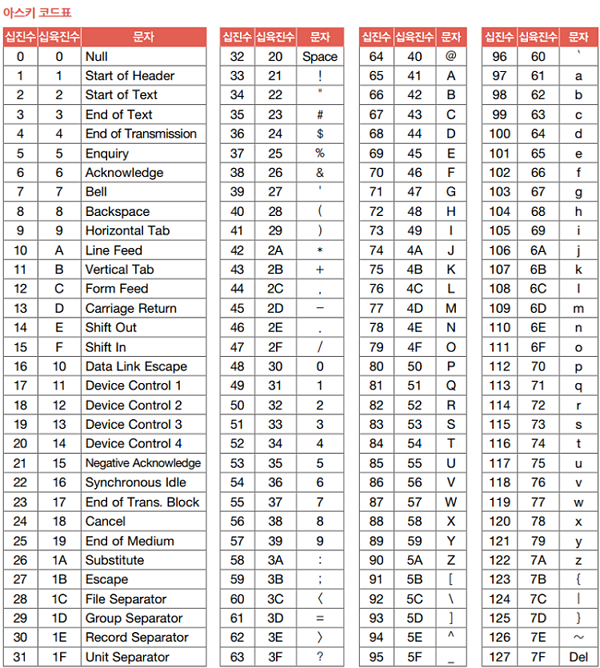
MySelf-Architec-Oper_2_14

위 표는 아스키 코드표입니다.

아스키 문자들은 0부터 127까지 총 128개의 숫자 중 하나의 고유한 수에 일대일로 대응됩니다.
아스키 문자에 대응된 고유한 수를 아스키 코드라고 합니다.
아스키 코드를 2진수로 표현함으로써 아스키 문자를 0과 1로 표현할 수 있습니다.
아스키 문자는 이렇게 아스키 코드로 인코딩됩니다.
e.g. ‘A’는 10진수 65로 인코딩되고, ‘a’는 10진수 97로, 특수 문자 !는 10진수 33으로 인코딩됩니다.
표를 보면 Backspace, Escape, Cancel, Space와 같은 제어 문자도 아스키 코드에 포함되어 있음

💡 코드 포인트(code point)

code point : 글자에 부여된 고유한 값

e.g. 아스키 문자 A의 코드 포인트는 65

쉬운 설명을 위해 코드 포인트라는 용어 대신 문자에 부여된 값, 문자에 부여된 코드라는 용어로 설명

아스키 코드는 간단하게 인코딩된다는 장점이 있지만, 단점도 있습니다.

한글을 표현할 수 없습니다.
한글뿐만 아니라 아스키 문자 집합 외의 문자, 특수문자도 표현할 수 없습니다.
근본적으로 아스키 문자 집합에 속한 문자들은 7비트로 표현하기에 128개보다 많은 문자를 표현못함
훗날 더 다양한 문자 표현을 위해 아스키 코드에 1비트를 추가한 8비트의 **확장 아스키(Extended ASCII)**가 등장
그럼에도 표현 가능한 문자의 수는 256개여서 턱없이 부족했습니다.
한국같은 비영어권 나라들은 자신들의 언어를 0과 1로 표현할 수 있는 고유 문자 집합과 인코딩 방식이 필요
이런 이유로 등장한 한글 인코딩 방식이 바로 EUC-KR입니다.

2.3 EUC-KR

한글 인코딩을 이해하려면 우선 한글의 특수성을 알아야 합니다. 알파벳을 쭉 이어 쓰면 단어가 되는 영어와는 달리, 한글은 각 음절 하나하나가 초성, 중성, 종성의 조합으로 이루어져 있습니다. 그래서 한글 인코딩에는 두 가지 방식, **완성형(한글 완성형 인코딩)**과 **조합형(한글 조합형 인코딩)**이 존재합니다.

완성형 인코딩 방식
- 초성, 중성, 종성의 조합으로 이루어진 완성된 하나의 글자에 고유한 코드를 부여하는 인코딩 방식
- e.g. ‘가’는 1, ‘나’는 2, ‘다’는 3, 이런 식으로 인코딩하는 방식
조합형 인코딩 방식
- 초성을 위한 비트열, 중성을 위한 비트열, 종성을 위한 비트열을 할당하여,
- 그것들의 조합으로 하나의 글자 코드를 완성하는 인코딩 방식
- 다시 말해 초성, 중성, 종성에 해당하는 코드를 합하여 하나의 글자 코드를 만드는 인코딩 방식

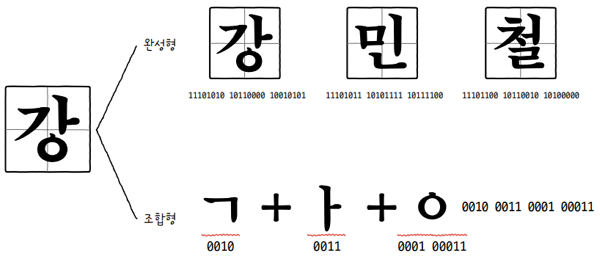
MySelf-Architec-Oper_2_15

EUC-KR은 KS X 1001, KS X 1003이라는 문자 집합을 기반으로 하는 대표적인 완성형 인코딩 방식입니다. 즉, EUC-KR 인코딩은 초성, 중성, 종성이 모두 결합된 한글 단어에 2바이트 크기의 코드를 부여합니다.

KS X 1001, KS X 1003 문자 집합은 외울 필요가 없습니다.

한글 한 글자에 2바이트 코드가 부여된다고 했죠? 다시 말해, EUC-KR로 인코딩된 한글 한 글자를 표현하려면 16비트가 필요합니다. 그리고 16비트는 네 자리 16진수로 표현할 수 있습니다. 즉, EUC-KR로 인코딩된 한글은 네 자리 16진수로 나타낼 수 있습니다.

MySelf-Architec-Oper_2_16

위 그림은 EUC-KR로 인코딩된 한글 일부를 나타냅니다.

‘가’의 경우 b0a0행의 두 번째 열인 b0a1로 인코딩되고,
‘거’의 경우 b0c0행의 여섯 번째 열인 $b0c5_{(16)}$ 로 인코딩됩니다.

EUC-KR 인코딩 방식으로 총 2,350개 정도의 한글 단어를 표현할 수 있습니다. 아스키 코드보다 표현할 수 있는 문자가 많아졌지만, 사실 이는 모든 한글 조합을 표현할 수 있을 정도로 많은 양은 아닙니다. 그래서 문자 집합에 정의되지 않은 ‘뷁 ’같은 글자는 EUC-KR로 표현할 수 없습니다.

모든 한글을 표현할 수 없다는 사실은 때때로 크고 작은 문제를 유발합니다. EUC-KR 인코딩을 사용하는 웹사이트의 한글이 깨진다든지, EUC-KR 방식으로는 표현할 수 없는 이름으로 인해 은행, 학교 등에서 피해를 받는 사람이 생겨나기도 했습니다.

이러한 문제를 조금이나마 해결하기 위해 등장한 것이 마이크로소프트의 CP949(Code Page 949)입니다. CP949는 EUC-KR의 확장된 버전으로, EUC-KR로는 표현할 수 없는 다양한 문자를 표현할 수 있습니다. 다만, 이마저도 한글 전체를 표현하기에 넉넉한 양은 아닙니다

2.4 유니코드와 UTF-8

EUC-KR 인코딩 덕분에 한국어를 코드로 표현할 수 있게 되었습니다.
하지만 모든 한글을 표현할 수 없다는 한계가 있었죠.
더욱이 이렇게 언어별로 인코딩을 나라마다 해야 한다면,
다국어를 지원하는 프로그램을 만들 때 나라 언어의 인코딩을 모두 알아야 하는 번거로움이 있습니다.
e.g. 한국어, 영어, 일본어, 중국어, 독일어를 지원하는 웹사이트가 있다면
- 이 웹사이트는 다섯 개 언어의 인코딩 방식을 모두 이해하고 지원해야 합니다.

그런데 만약 모든 나라 언어의 문자 집합과 인코딩 방식이 통일되어 있다면,

다시 말해 모든 언어를 아우르는 문자 집합과 통일된 표준 인코딩 방식이 있다면
- 언어별로 인코딩하는 수고로움을 덜 수 있을 겁니다.
그래서 등장한 것이 유니코드(unicode) 문자 집합입니다.
- 유니코드 = 여러 나라의 문자를 광범위하게 표현할 수 있는 통일된 문자 집합
유니코드는 EUC-KR보다 훨씬 다양한 한글을 포함하며
대부분 나라의 문자, 특수문자, 화살표나 이모티콘까지도 코드로 표현할 수 있는 통일된 문자 집합입니다.
유니코드는 현대 문자를 표현할 때 가장 많이 사용되는 표준 문자 집합이며,
문자 인코딩 세계에서 매우 중요한 역할을 맡고 있습니다.

예시와 함께 학습해 봅시다. 유니코드 문자 집합에서 ‘한’과 ‘글’이라는 단어를 찾아 볼까요? 아래 링크에서 찾을 수 있습니다.

http://www.unicode.org/charts/PDF/UAC00.pdf

MySelf-Architec-Oper_2_17

유니코드 문자 집합에서는 아스키 코드나 EUC-KR과 같이 각 문자마다 고유한 값이 부여됩니다. 예를 들어, ‘한’에 부여된 값은 $D55C_{(16)}$ , ‘글’에 부여된 값은 $AE00_{(16)}$ 입니다.

💡 간혹 유니코드 글자에 부여된 값 앞에 U+D55C, U+AE00처럼 U+라는 문자열을 붙이기도 하는데, 이는 16진수로 유니코드를 표현할 때 사용하는 표기입니다.

아스키 코드나 EUC-KR은 글자에 부여된 값을 그대로 인코딩 값으로 삼았죠? 유니코드는 조금 다릅니다.

글자에 부여된 값 자체를 인코딩된 값으로 삼지 않고 이 값을 다양한 방법으로 인코딩합니다.
이런 인코딩 방법에는 크게 UTF-8, UTF-16, UTF-32 등이 있습니다.
요컨대 UTF-8, UTF-16, UTF-32는 유니코드 문자에 부여된 값을 인코딩하는 방식입니다.

💡 UTF는 Unicode Transformation Format의 약어로 유니코드를 인코딩하는 방법입니다.

가장 대중적인 UTF-8에 대해 알아보겠습니다. 인코딩하는 방식을 외우지 말고, 그저 문자가 0과 1로 어떻게 표현되는지 감상하는 기분으로 가볍게 읽으면 됩니다.

UTF-8은 통상 1바이트부터 4바이트까지의 인코딩 결과를 만들어 냅니다.

다시 말해 UTF-8로 인코딩한 값의 결과는 1바이트가 될 수도
2바이트, 3바이트, 4바이트가 될 수도 있습니다.
UTF-8로 인코딩한 결과가 몇 바이트가 될지는 유니코드 문자에 부여된 값의 범위에 따라 결정됩니다.

다음 표를 볼까요?

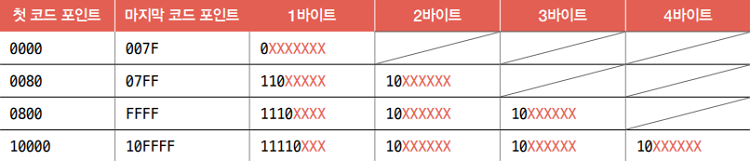
MySelf-Architec-Oper_2_18

유니코드 문자에 부여된 값의 범위가 0부터 $007F_{(16)}$ 까지는 1바이트로 표현
유니코드 문자에 부여된 값의 범위가 $0080_{(16)}$ 부터 $07FF_{(16)}$ 까지는 2바이트로 표현
유니코드 문자에 부여된 값의 범위가 $0800_{(16)}$ 부터 $FFFF_{(16)}$ 까지는 3바이트로 표현
유니코드 문자에 부여된 값의 범위가 $10000_{(16)}$ 부터 $10FFFF_{(16)}$ 까지는 4바이트로 표현

그렇다면 ‘한글’은 몇 바이트로 구성될까요? ‘한’에 부여된 값은 $D55C_{(16)}$ , ‘글’에 부여된 값은 $AE00_{(16)}$ 이었죠? 두 글자 모두 $0800_{(16)}$ 와 $FFFF_{(16)}$ 사이에 있네요. 따라서 ‘한’과 ‘글’을 UTF-8로 인코딩하면 3바이트로 표현될 것을 예상할 수 있습니다.

다시 표를 봅시다. 3바이트로 인코딩된 값은 다음과 같은 형태를 띈다고 되어 있죠?

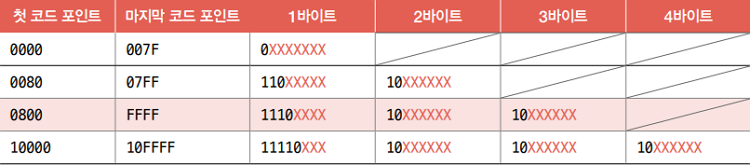
MySelf-Architec-Oper_2_19

여기서 붉은색 X표가 있는 곳에 유니코드 문자에 부여된 고유한 값이 들어갑니다.
‘한’과 ‘글’에 부여 된 값은 각각 $D55C_{(16)}$ , $AE00_{(16)}$ 였습니다.
이는 각각 이진수로 1101 0101 0101 1100, 1010 1110 0000 0000입니다.

따라서 UTF-8 방식으로 인코딩된 값은 다음과 같습니다. 이 수가 ‘한’ 과 ‘글’의 UTF-8 방식으로 인코딩한 결과입니다.

111101101 10010101 10011100(2)
211101010 10111000 10000000(2)

지금까지 다양한 문자들을 0과 1로 표현하는 방법에 대해 알아보았습니다. 생각보다 간단하죠?

2.5 핵심 포인트

문자 집합은 컴퓨터가 인식할 수 있는 문자의 모음으로,
- 문자 집합에 속한 문자를 인코딩하여 0과 1로 표현할 수 있습니다.
아스키 문자 집합에 0부터 127까지의 수가 할당되어 아스키 코드로 인코딩됩니다.
EUC-KR은 한글을 2바이트 크기로 인코딩할 수 있는 완성형 인코딩 방식입니다.
유니코드는 여러 나라의 문자들을 광범위하게 표현할 수 있는 통일된 문자 집합이며, UTF-8, UTF-16, UTF-32는 유니코드 문자의 인코딩 방식입니다.

2.6 확인 문제

Q1 68쪽의 아스키 코드표를 참고하여 아래의 아스키 코드를 디코딩한 내용을 써 보세요.

1104 111 110 103 111 110 103 → ( )

Q2 다음 중 EUC-KR 인코딩에 대한 설명 중 옳지 않은 것을 고르세요.

한국어를 표현할 수 있는 인코딩 방식입니다.
조합형 인코딩 방식입니다.
하나의 완성된 한글 글자에 코드를 부여합니다.
모든 한글을 표현할 수 없습니다.

Q3 유니코드 문자 집합에서 ‘안’에 부여된 값은 $C548_{(16)}$ , ‘녕’에 부여된 값은 $B155_{(16)}$ 입니다. ‘안녕’을 UTF-8로 인코딩한 값을 구해 보세요.

01-컴퓨터 구조 03-명령어