1. 교착 상태(deadlock)
위 그림처럼 도심 속 도로에서 차가 꽉 막혀 꼼짝달싹 못하는 상황을 보신 적이 있을 겁니다. 이렇게 교통이 마비되어 버리면 복구되기까지 오랜 시간이 걸릴 뿐더러, 심한 경우 교통 경찰이 직접 와서 마비를 해결해야 합니다.
프로세스 실행 과정에도 이와 비슷한 문제가 있습니다.
- 프로세스를 실행하기 위해서는 자원이 필요한데,
- 2개 이상의 프로세스가 각자 가지고 있는 자원을 무작정 기다린다면,
- 그 어떤 프로세스도 더 이상 진행할 수 없는
교착 상태가 됩니다. - 교착 상태는 정확히 무엇이며, 언제 어떻게 발생하는지 알아보겠습니다.
1.1 식사하는 철학자 문제
식사하는 철학자 문제(dining philosophers problem)는 교착 상태를 설명하기 위한 고전적이고 재미있는 문제 상황입니다.
- 이 유명한 문제는 교착 상태가 어떤 상황에서 왜 발생하는지,
- 나아가 교착 상태를 어떻게 해결할 수 있는지를 엿볼 수 있는 가상의 문제 시나리오입니다.
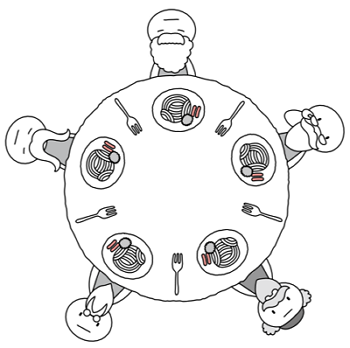
자, 동그란 원탁에 다섯 명의 철학자가 앉아 있습니다.
- 이 철학자들 앞에는 맛있는 식사가 있고,
- 철학자들 사이 사이에는 식사에 필요한 포크가 있습니다.
- 그리고 철학자들 앞에 있는 식사는 2개의 포크로 먹을 수 있는 음식이라 가정하겠습니다
그리고 이 철학자들은 다음과 같은 순서로 식사를 합니다.
- 계속 생각을 하다가 왼쪽 포크가 사용 가능하면 집어든다.
- 계속 생각을 하다가 오른쪽 포크가 사용 가능하면 집어든다.
- 왼쪽과 오른쪽 포크를 모두 집어들면, 정해진 시간동안 식사를 한다.
- 식사 시간이 끝나면 오른쪽 포크를 내려놓는다.
- 오른쪽 포크를 내려놓은 뒤 왼쪽 포크를 내려놓는다.
- 다시 1번부터 반복한다.
과연 이 철학자들은 식사를 무사히 마칠 수 있을까요?
- 언뜻 보면 위 순서에는 아무런 문제가 없어 보입니다.
- 실제로도 한두 명의 철학자가 식사할 때는 아무런 문제가 없습니다.
하지만 모든 철학자가 동시에 포크를 집어 식사를 하면,
- 어떤 철학자도 식사를 할 수 없고, 영원히 생각만 하는 상황이 발생할 수 있습니다.
- 모든 철학자가 왼쪽 포크를 집어들면, 모두가 오른쪽 포크를 집어 들 수 없기 때문이죠.
- 다시 말해, 모든 철학자는 다른 철학자가 포크를 내려놓을 때까지 기다립니다.
- 이렇게 일어나지 않을 사건을 기다리며 진행이 멈춰버리는 현상을
교착 상태(deadlock)라고 합니다.
식사하는 철학자 문제에서 철학자는
- 프로세스 혹은 스레드,
포크는 자원,생각하는 행위는 자원을 기다리는 것에 빗대어 볼 수 있습니다. - 그리고
포크는 한 번에 하나의 프로세스 혹은 스레드만 접근할 수 있으니 임계 구역이라고 볼 수 있지요.
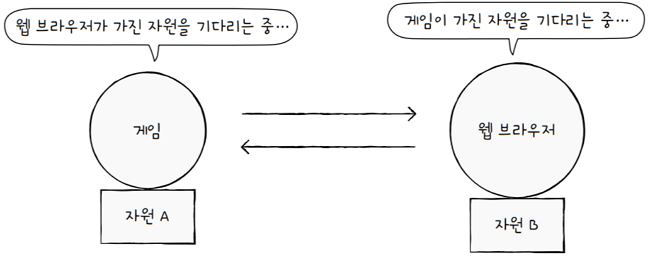
-
이는 마치
게임 프로세스는자원 A를 점유한 채,웹 브라우저 프로세스가 점유하고 있는자원 B의 사용이 끝나길 기다리고,
-
웹 브라우저 프로세스는자원 B를 점유한 채,게임 프로세스의 자원 A 사용이 끝나길 기다리는 상황과 같습니다.
-
이 경우
게임과웹 브라우저 프로세스는 상대방이 가진 자원을 기다리기만 하다가,- 결국 실행 한 번 못하는 상황이 벌어집니다.
- 이를
교착 상태라고 합니다.

교착 상태는 아주 다양한 상황에서 발생합니다. 앞서 배운 뮤텍스 락에서도 교착 상태는 발생할 수 있습니다.
-
e.g. 프로세스 A는 임계 구역 진입 전 lock1을 잠그고(
lock1 = true;),- 프로세스 B는 임계 구역 진입 전 lock2를 잠갔다고(
lock2 = true;) 가정해 보겠습니다.
- 프로세스 B는 임계 구역 진입 전 lock2를 잠갔다고(
-
만일
프로세스 A는 lock2가 false가 되길 기다리고, -
프로세스 B는 lock1이 false가 되길 기다린다면 교착 상태가 발생합니다.
이러한 교착 상태를 해결하기 위해서는
- 첫째, 교착 상태가 발생했을 때의 상황을 정확히 표현해보고,
- 둘째, 교착 상태가 일어나는 근본적인 이유에 대해 알아야 합니다.
그렇다면 우선 교착 상태가 발생했을 때의 상황을 한 눈에 보기 쉽게 그래프로 표현하는 방법부터 알아보도록 합시다.
1.2 자원 할당 그래프
- 교착 상태는
자원 할당 그래프(resource-allocation graph)를 통해 단순하게 표현 가능합니다. - 교착 상태 발생 조건 파악 가능
- 어떤 프로세스가 어떤 자원을 할당받아 사용 중인지 확인 가능
- 어떤 프로세스가 어떤 자원을 기다리고 있는지 확인 가능
자원 할당 그래프는 다음과 같은 규칙으로 그려집니다.
첫째,
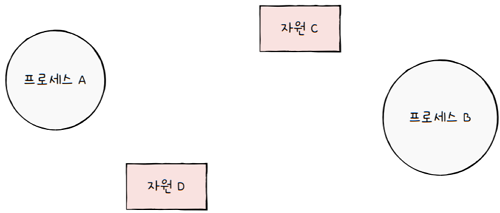
프로세스는 원으로, 자원의 종류는 사각형으로 표현합니다.
둘째,
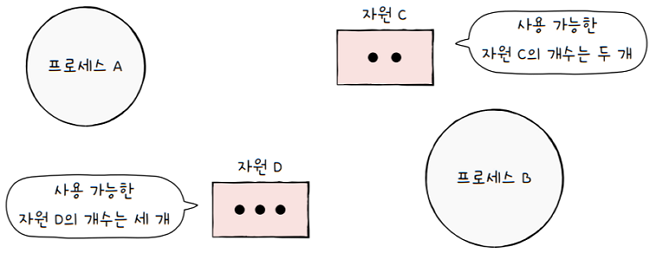
사용할 수 있는 자원의 개수는 자원 사각형 내에 점으로 표현합니다.
- 같은 자원이라 할지라도, 사용 가능한 자원의 개수는 여러 개 있을 수 있습니다.
- e.g. HDD가 3개 있는 경우,
- 자원의 종류는 HDD 1개이지만, 사용 가능한 HDD 수는 3개
- 따라서 HDD는 사각형 안에 세 개의 점으로 표현
- e.g. CPU가 2개 있는 경우,
- 자원의 종류는 CPU 1개이지만, 사용 가능한 CPU 개수는 2개
- 따라서 CPU 사각형 안에 2개의 점으로 표현
셋째,
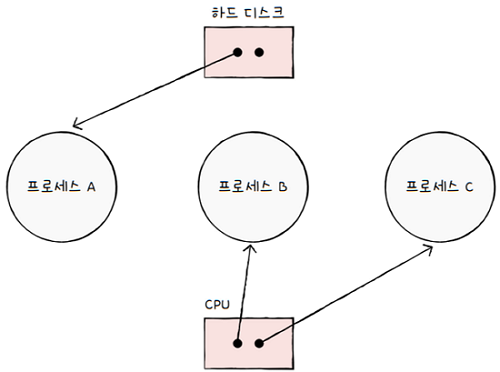
프로세스가 어떤 자원을 할당받아 사용 중이라면, 자원에서 프로세스를 향해 화살표를 표시합니다.
- e.g. 위 그림은
HDD 자원 하나는 프로세스 A에 할당되었고,CPU는 각각 프로세스 B, C 에 할당되었음을 표현
프로세스가 자원 이용을 끝내고, 운영체제에 자원을 반납하면 화살표는 삭제됩니다.
넷째,
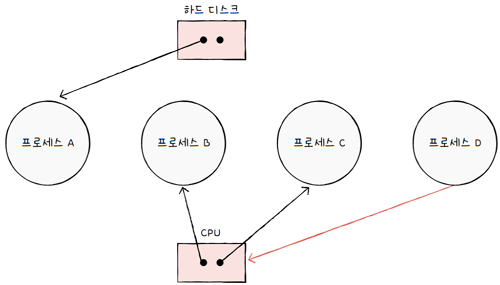
프로세스가 어떤 자원을 기다리고 있다면, 프로세스에서 자원으로 화살표를 표시합니다.
- e.g. 위 그림은
프로세스 D가 CPU의 할당을 기다리고 있음을 표현
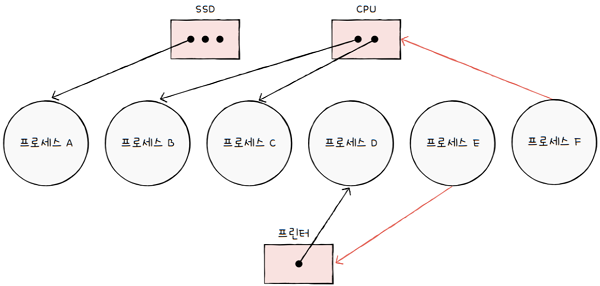
생각보다 간단하죠? 간단한 예를 하나 더 봅시다. 위와 같은 자원 할당 그래프는 무엇을 의미할까요?
- 현재 사용 가능한
SSD 자원은 3개,CPU 자원은 2개,프린터는 1개있는데, 프로세스 A는 SSD를 할당받아 사용 중이고,프로세스 B와 C는 CPU를 할당받아 사용 중이며,프로세스 D는 프린터를 사용 중이다.프로세스 E는 프린터의 할당을 기다리고 있고,프로세스 F는 CPU의 할당을 기다리고 있다라고 볼 수 있습니다.
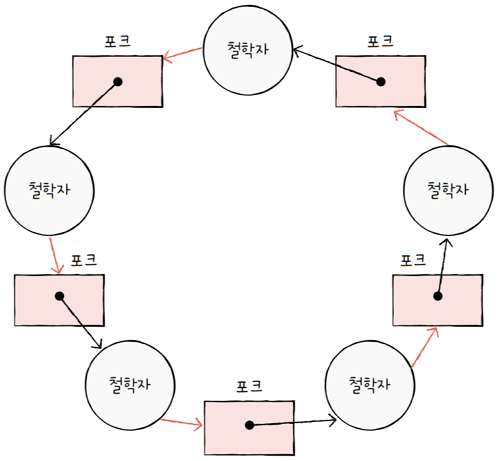
앞서 설명한 식사하는 철학자 문제도 자원 할당 그래프로 표현해보면,
- 식사하는 철학자 문제에서
포크는 자원,철학자는 프로세스와 같다고 했습니다. - 식사하는 철학자 문제는 모든 철학자가 왼쪽 포크를 든 채,
- 오른쪽 포크를 기다리고 있는 상황이니 위 그림과 같이 표현할 수 있습니다.
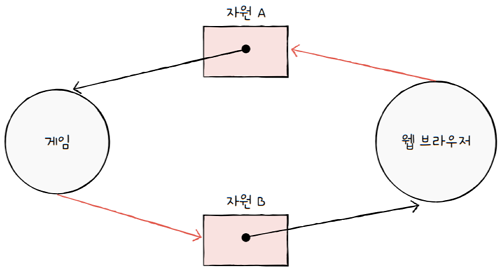
또 다른 교착 상태를 자원 할당 그래프로 표현해보면,
게임 프로세스는자원 A를 할당받은 채,- 웹 브라우저 프로세스가 할당받은 자원 B의 사용이 끝나길 기다리고 있고,
웹 브라우저 프로세스는자원 B를 할당받은 채,- 게임 프로세스가 할당받은 자원 A의 사용이 끝나길 기다리는 상황입니다.
눈치가 빠른 독자라면 벌써 교착 상태가 일어난 그래프의 특징을 눈치챘을 것입니다.
교착 상태가 발생한 상황은 자원 할당 그래프가 원의 형태를 띄고 있습니다.
그럼 이제 교착 상태가 발생하는 근본적인 이유에 대해 자세히 알아보겠습니다.
1.3 교착 상태 발생 조건
다시 식사하는 철학자 문제로 돌아와 봅시다. 이러한 교착 상태는 왜 발생했을까요? 교착 상태가 발 생할 조건에는 4가지가 있습니다.
상호 배제(mutual exclusion)- 한 프로세스가 사용하는 자원을 다른 프로세스가 사용할 수 없는 상태
- 교착 상태가 발생한 근본적인 원인은 해당 자원을 한 번에 하나의 프로세스만 이용 가능했기 때문
- e.g. 식사하는 철학자 문제에서 하나의 포크를 여러 명이 동시에 사용할 수 있었다면 교착 상태는 발생X
점유와 대기(hold and wait)- 자원을 할당받은 상태에서 다른 자원을 할당받기를 기다리는 상태
- 자원을 보유한 채 다른 자원을 기다렸기 때문에 문제가 발생
- e.g. 식사하는 철학자 문제에서 누구도 식사를 이어나갈 수 없었던 이유는
- ‘왼쪽 포크를 들고’ 다른 철학 자의 포크를 기다렸기 때문
비선점(nonpreemptive)- 어떤 프로세스도 다른 프로세스의 자원을 강제로 빼앗지 못하는 상태
- 교착상태가 발생한 근본적인 문제는 프로세스가 자원을 비선점하고 있었기 때문
- 즉, 어떤 프로세스도 다른 프로세스의 자원을 강제로 빼앗지 못함
- e.g. 철학자들 중 누군가가 다른 철학자의 포크를 강제로 빼앗을 수 있었다면 교착 상태는 발생X
- but 철학자들은 모두 점잖게 그저 포크를 기다리기만 해서 교착상태 발생
원형 대기(circular wait)- 프로세스들이 원의 형태로 자원을 대기하는 상태
- 프로세스들과 프로세스가 요청 및 할당받은 자원이 원의 형태를 이루었기 때문
- 다시 말해, 자원 할당 그래프가 원의 형태로 그려지면 교착 상태가 발생
💡 원형 대기라고 무조건 교착상태가 발생하는 것은 아니다.
자원 할당 그래프가 원의 형태로 그려지면 교착 상태가 발생할 ‘수’ 있다고 표현한 이유가 있습니다.
- 자원 할당 그래프가 원의 형태를 띄지 않는다면, 교착 상태는 발생하지 않으나,
- 원의 형태를 띈다고 해서 반드시 교착 상태가 발생하는 것은 아닙니다.
즉, 위 4가지 조건 중 하나라도 만족하지 않는다면, 교착 상태가 발생하지 않지만, 위 조건이 모두 만족될 때, 교착 상태가 발생할 가능성이 생긴다고 보면 됩니다.
2. 교착 상태 해결 방법
교착 상태는 마치 차로 꽉 찬 도로처럼 꼼짝도 못하는 상황이라고 했습니다. 운영체제는 이러한 교착 상태를 어떻게 해결할까요? 크게 3가지 방법이 있습니다.
- 예방
- 회피
- 검출 후 회복
2.1 교착 상태 예방
- 애초에 교착 상태가 발생하지 않도록
- 교착 상태 발생 조건(상호 배재, 점유와 대기, 비선점, 원형 대기) 중 하나를 없애버리기
- cf. 교착 상태 발생 조건 중 하나의 조건이라도 만족하지 않으면, 교착 상태는 발생하지 않습니다.
2.1.1 상호배재를 없애면?
우선 자원의 상호 배제를 없애볼까요?
- 자원의 상호 배제를 없앤다는 말의 의미는 **‘모든 자원을 공유 가능하게 만든다’**는 말과 같습니다.
- 다만 이 방식대로면 이론적으로는 교착 상태를 없앨 수 있지만,
- 현실적으로 모든 자원의 상호 배제를 없애기는 어렵기에
- 이 방식을 현실에서 사용하기에는 다소 무리가 있습니다.
2.1.2 점유와 대기를 없애면?
- 특정 프로세스에 자원을 모두 할당하거나, 아예 할당하지 않는 방식으로 배분
- e.g. 식사하는 철학자 문제 속 철학자들이 한 손에 포크를 들고, 다른 포크를 기다리지 못하게 금지하는 것
- 포크를 두 개 동시에 들게 하거나, 아니면 아예 들지 못하게 하는 것
- 이 방식도 이론적으로는 교착 상태를 해결할 수 있지만, 단점도 있습니다.
- 단점 : 자원의 활용률을 낮출 수 있는 방식
점유와 대기를 금지하면,
한 프로세스에 필요한 자원들을 몰아주고,- 그 다음에
다른 프로세스에 필요한 자원들을 몰아주는 방식
- 그 다음에
자원이 필요해도 기다릴 수밖에 없는 프로세스와사용되지 않으면서 오랫동안 할당되는 자원을 다수 양산
- 많은 자원을 사용하는 프로세스가 불리
자원을 많이 사용하는 프로세스는자원을 적게 사용하는 프로세스에 비해- 동시에 자원을 사용할 타이밍을 확보하기가 어러움
- 이는 결국 많은 자원을 필요로 하는 프로세스가 무한정 기다리게 되는 기아 현상을 야기
2.1.3 비선점 조건을 없애면?
- 자원을 이용 중인 프로세스로부터 해당 자원을 빼앗을 수 있습니다.
- 이는 선점이 가능한 자원(e.g. CPU)에 한해서 효과적
- e.g. 철학자 문제에서 철학자의 포크를 빼앗을 수만 있다면, 교착 상태는 발생X
- e.g.
한 프로세스가 CPU를 이용하다가 일정 시간이 지나면,- 아직 작업이 모두 끝나지 않았다고 해도,
다른 프로세스가 CPU를 할당받아 사용
- 아직 작업이 모두 끝나지 않았다고 해도,
- 그러나 모든 자원이 선점 가능한 것은 아닙니다.
- e.g. 한 번에 하나의 프로세스만 이용 가능 한 프린터 자원이 있다고 가정
- 한 프로세스가 프린터를 이용하는 도중, 다른 프로세스가 프린터 자원을 빼앗아 사용하기 어려움
- 비선점 조건을 없애 모든 자원을 빼앗을 수 있도록 하여
- 교착 상태를 예방하는 방법은 다소 범용성이 떨어지는 방안
2.1.4 원형 대기 조건을 없애면?
- 원형 대기를 없애는 방법은 간단합니다.
- 모든 자원에 번호를 붙이고, 오름차순으로 자원을 할당하면, 원형 대기는 발생하지 않습니다.
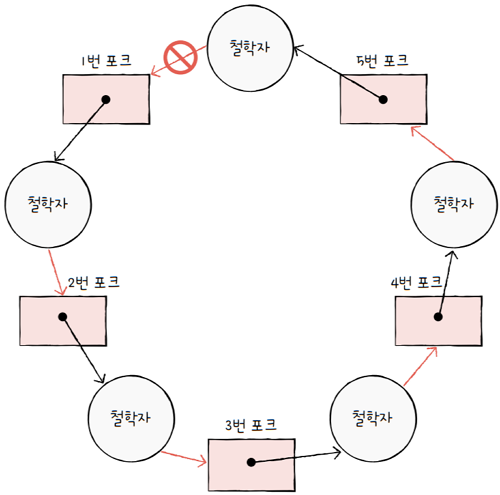
e.g. 식사하는 철학자 문제에서 모든 포크에 1번부터 5번까지 번호를 붙이고,
- 철학자들로 하여금 번호가 낮은 포크에서 높은 포크 순으로 집어들게 한다면 원형 대기는 발생하지 않습니다.
- 5번 포크를 집어들고 1번 포크를 집어들 수 없기 때문이지요.
이는 마치 철학자들이 원형 식탁이 아닌 사각형 식탁에서 일렬로 앉아 식사하는 상황과 유사합니다. 이 경우 철학자들이 동시에 포크를 들어도 문제될 것이 없습니다.
- 원형 대기를 없앰으로써 교착 상태를 예방하는 방식은
- 앞선 세 방식에 비하면 비교적 현실적이고 실용적인 방식이지만, 역시 단점은 있습니다.
- 모든 컴퓨터 시스템 내에 존재하는 수많은 자원에 번호를 붙이는 일은 어려운 작업이기도 하고,
- 각 자원에 어떤 번호를 붙이는지에 따라 특정 자원의 활용률이 떨어질 수 있습니다.
이렇듯 교착 상태의 발생 조건을 원천적으로 제거하여,
교착 상태를 사전에 방지하는 예방 방식은
교착 상태가 발생하지 않음을 보장할 수는 있지만, 여러 부작용이 따릅니다.
2.2 교착 상태 회피
- 교착 상태를 무분별한 자원 할당으로 인해 발생했다고 간주
- 교착 상태가 발생하지 않을만큼 조심 조심 할당하기
- 배분할 수 있는 자원의 양을 고려하여, 교착 상태가 발생하지 않을 만큼만 자원 배분
- e.g. 식사하는 철학자 문제
- 포크가 100개 있는 상태에서 철학자들이 한두 개 의 포크를 요구하면 교착 상태는 발생X
- 반면 포크의 양이 충분하지 않은 상태에서 모두 최대의 포크(2개)를 요구하면, 교착 상태가 발생
2.2.1 3가지 용어
교착 상태를 회피하는 방법을 학습하기 위해서는 다음 3가지 용어를 알아야 합니다.
안전 순서열(safe sequence)- 교착 상태없이 안전하게 모든 프로세스들에 자원을 할당할 수 있는 순서
- e.g. 웹 브라우저, 메모장, 게임 프로세스가 동시에 운영체제에 자원을 요청
- 웹 브라우저 → 메모장 → 게임 프로세스 순서대로 자원을 할당하면,
- 교착 상태가 발생하지 않는다고 가정
- 웹 브라우저 → 메모장 → 게임이
안전 순서열
안전 상태(safe state)- 교착 상태가 발생하지 않고 모든 프로세스가 정상적으로 자원을 할당받고 종료될 수 있는 상태
- 안전 순서열이 있는 상태를
안전 상태
불안전 상태(unsafe state)- 교착 상태가 발생할 수도 있는 상황
- 안전 순서열이 없는 상태를
불안전 상태 - cf. 시스템이 불안전 상태에 놓이면, 교착 상태가 발생할 수 있는 위험이 있습니다.
2.2.2 안전 상태 예시
안전 상태와 불안전 상태, 안전 순서열은 용어의 정의보다 예시를 통해 이해하는 것이 좋습니다.
- e.g. 컴퓨터 시스템에 총 12개 자원이 있고,
- 프로세스 P1, P2, P3가 각각 5개, 2개, 2개의 자원을 할당받아 실행 중
- 운영체제가 배분할 수 있는 자원의 개수는? 3개
- 프로세스 P1, P2, P3은 각각 최대 10개, 4개, 9개의 자원을 요구할 수 있다고 가정
현재 상황은 아래와 같이 간단한 표로 표현할 수 있습니다.
💡 안전 순서열이 존재 : P2 → P1 → P3
프로세스 요구량 현재사용량 P1 10 5 P2 4 2 P3 9 2
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 9
- 남은 자원(할당 가능 자원 - 할당한 자원): 3
이떄, 프로세스 P1, P2, P3이 모두 최대로 자원을 요구한 최악의 상황을 가정하면, (즉, P1, P2, P3이 각각 10개, 4개, 9개의 자원을 요구한 상황을 가정하면)
💡 P2는 이미 자원 2개를 가지고 있으므로, 남은 자원에서 2개를 배분하면 됩니다.
프로세스 최대 요구량 현재 사용량 P1 10 5 P2 4 2 + 2P3 9 2
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 9
+ 2 = 11- 남은 자원(할당 가능 자원 - 할당한 자원): 3
- 2 = 1
💡
요구한 4개의 자원을 할당받은 P2는 정상적으로 작업을 끝내고 가지고 있던 자원을 반환합니다. 그러면 남은 자원은 5개가 됩니다.
프로세스 최대 요구량 현재 사용량 P1 10 5 P2 4 2 + 2P3 9 2
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 11
- 4 = 7- 남은 자원(할당 가능 자원 - 할당한 자원): 1
+ 4 = 5
💡 P1에 남은 자원 5개를 할당하면, P1 또한 작업을 정상적으로 완료할 수 있습니다.
프로세스 최대 요구량 현재 사용량 P1 10 5 + 5P2 4 2 + 2(종료 및 자원 반환)P3 9 2
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 7
+ 5 = 12- 남은 자원(할당 가능 자원 - 할당한 자원): 5
- 5 = 0
💡 P1이 작업을 정상적으로 마치고 자원을 반환하면 이제 P3에 자원을 할당하면 됩니다
프로세스 최대 요구량 현재 사용량 P1 10 5 + 5(종료 및 자원 반환)P2 4 2 + 2(종료 및 자원 반환)P3 9 2
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 12
- 10 = 2- 남은 자원(할당 가능 자원 - 할당한 자원): 0
+ 10 = 10
즉, P2 → P1 → P3이라는 안전 순서열대로 자원을 배분하면,
P1, P2, P3 모두 자원을 할당받고, 교착상태없이 올바르게 작업을 마칠 수 있습니다.
2.2.3 불안전 상태 예시
이번에는 다른 상황을 가정해봅시다.
| 프로세스 | 최대 요구량 | 현재 사용량 |
|---|---|---|
| P1 | 10 | 5 |
| P2 | 4 | 2 |
| P3 | 9 | 2 |
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 10
- 남은 자원(할당 가능 자원 - 할당한 자원):
3
💡 위 상황에서 운영체제가 P3에게 선뜻 자원 하나를 내주었다면? ( 즉, 안전 순서열이 지켜지지 않은 경우라면 === 불안전 상태라면 )
프로세스 최대 요구량 현재 사용량 P1 10 5 P2 4 2 P3 9 3
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 10
- 남은 자원(할당 가능 자원 - 할당한 자원):
2
💡 이번에도, 프로세스 P1, P2, P3이 모두 최대로 자원을 요구한 최악의 상황을 가정하면, (즉, P1, P2, P3이 각각 10개, 4개, 9개의 자원을 요구한 상황을 가정하면)
프로세스 최대 요구량 현재 사용량 P1 10 5 P2 4 2 + 2 P3 9 3
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 10 + 2 = 12
- 남은 자원(할당 가능 자원 - 할당한 자원): 2 - 2 = 0
💡 P2에 2개의 자원을 배분하여, P2 작업을 올바르게 끝낸다고 해도, P2 작업 이후 반환된 자원 4개로는 P1의 요구도 P3의 요구도 들어줄 수 없습니다.
P1과 P3은 서로가 보유하고 있는 자원만을 바라보며, 무한정 기다릴 수밖에 없습니다. > 불안전 상태로 교착 상태가 발생한 것이지요.
프로세스 최대 요구량 현재 사용량 P1 10 5 P2 4 2 + 2 P3 9 3
- 할당 가능 자원: 12
- 할당한 자원(P1, P2, P3 현재 사용량의 총합): 12 - 4 = 8
- 남은 자원(할당 가능 자원 - 할당한 자원): 0 + 4 = 4
운영체제가 교착 상태를 회피하기 위해서는 (즉, 교착상태 회피 방식은)
- 안전 상태에서 안전 상태로 움직이는 경우에만 자원을 할당하는 방식
- 항시 안전 상태를 유지하도록 자원을 할당하는 방식
- cf. 은행원 알고리즘
2.3 교착 상태 검출 후 회복
- cf.
교착 상태 예방과회피는 교착 상태 발생을 막기 위한 노력 - 교착 상태 발생을 인정하고, 사후에 조치하는 방식
- 프로세스들이 자원을 요구하면 일단 할당하고, 교착상태가 검출되면 회복
- 회복하는 방법에는 다음 2가지 방식이 있습니다.
선점을 통한 회복프로세스 강제 종료를 통한 회복
2.3.1 선점을 통한 회복
- 교착 상태가 해결될 때까지 한 프로세스씩 자원을 몰아주는 방식
- 즉, 교착 상태가 해결될 때까지, 다른 프로세스로부터 자원을 강제로 빼앗고, 한 프로세스에 할당하는 방식
2.3.2 프로세스 강제 종료를 통한 회복
- 가장 단순하면서 확실한 방식
- 교착 상태에 놓인 프로세스를 모두 강제 종료하고,
- (많은 프로세스들이 작업 내역을 잃을 위험성이 존재)
- 교착 상태가 해결될 때까지 한 프로세스씩 강제 종료
- (작업 내역을 잃는 프로세스는 최대한 줄일 수 있지만,
- 교착 상태가 없어졌는지 여부를 확인하는 과정에서 오버헤드를 야기)
2.4 여담 : 교착 상태 무시
지금까지 교착 상태와 해결 방법에 대해 알아보았습니다.
마지막 여담을 이야기하자면, 실은 교착 상태를 아예 무시하는 방법도 있습니다.
드물게 발생하는 잠재적 문제를 무시로 대처하는 방식으로
타조 알고리즘(ostrich algorithm)이라는 거창한 이름을 가진 방식이지요.

💡 참고
타조가 문제에 처했을 때 머리를 땅에 묻고 모른 체하는 모습에서 따온 이름이지만, 실제로 타조가 이렇게 행동하지는 않습니다
완벽을 추구하는 과학자나 수학자 입장에서는 납득할 수 없는 방식일지 모르나, 문제 발생의 빈도나 심각성에 따라 최대 효율을 추구하는 엔지니어 입장에서는 때때로 이 방식이 적합할 때도 많습니다.