1. 트리(Tree)

방향 그래프의 일종으로 정점을 가리키는 간선이 하나 밖에 없는 구조를 가지고 있다.
- e.g. 디렉토리(폴더) 구조
- e.g. 회사 조직도

1.1 트리 용어

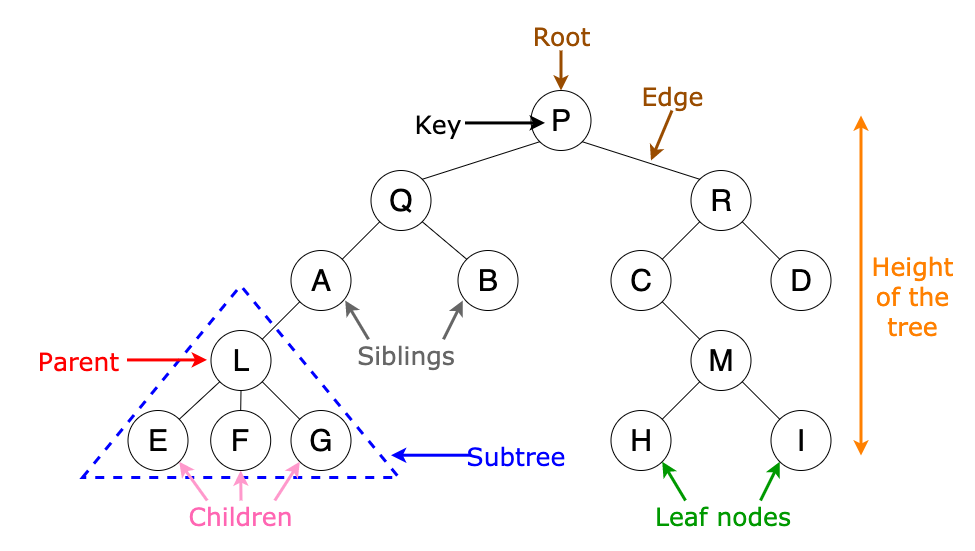
Data Structure_9_1

Node : 트리의 구성요소, 트리 구조를 이루는 모든 개별 데이터
- 부모 노드(Parent node), 자식 노드(Child node)
Root : 트리의 최상위 Node
리프(Leaf) : 트리 구조의 끝지점이고, 자식 노드가 없는 노드
깊이 (depth) : 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 표현
레벨(Level) : 트리 구조에서 같은 깊이를 가지고 있는 **노드를 묶어서 레벨(level)**로 표현
Leaf Node : 트리의 깊이 단계
Sub tree : 트리 구조에서 root에서 뻗어나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리

1.2 트리의 특징

루트 정점을 제외한 모든 정점은 하나의 부모 정점을 가진다.
정점이 N개인 트리는 반드시 N-1개의 간선을 가진다.
루트에서 특정 정점으로 가는 경로는 유일하다.

1.3 트리의 구현 방법

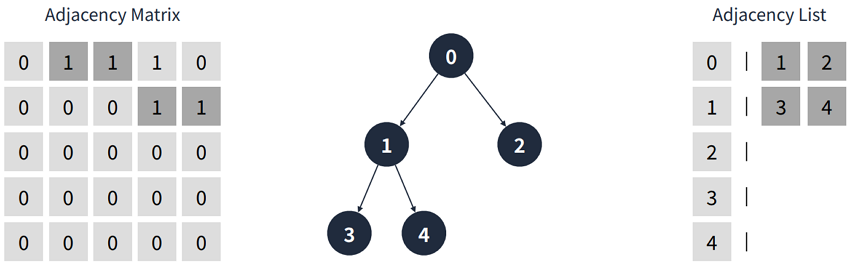
그래프와 마찬가지로 인접 행렬, 인접 리스트 두 가지 방식으로 트리를 표현할 수 있다.

Data Structure_9_2

2. 이진 트리

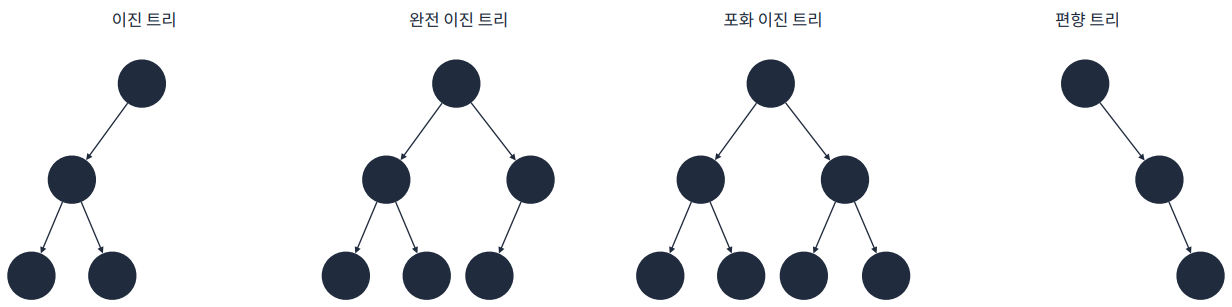
Data Structure_9_3

이진 트리는 각 정점이 최대 2개의 자식을 가지는 트리를 의미한다.
완전 이진 트리는 마지막 레벨을 제외하고 모든 정점이 채워진 트리를 의미한다.
포화 이진 트리는 마지막 레벨까지 모든 정점이 채워진 트리를 의미한다.
편향 트리는 한 방향으로만 정점이 이어지는 트리를 의미한다.

2.1 이진 트리의 특징

정점이 N개인 이진 트리는 최악의 경우 높이가 N이 될 수 있다.
정점이 N개인 포화 또는 완전 이진트리의 높이는 $log\ N$ 이다.
높이가 h인 포화 이진 트리는 $2^h -1$ 개의 정점을 갖는다.
일반적인 이진 트리를 사용하는 경우는 많지 않다. 다음 자료구조에 응용된다.
- 이진 탐색 트리
- 힙
- AVL 트리
- 레드 블랙 트리

2.2 이진 트리의 구현 방법

배열 혹은 요소에 링크가 2개 존재하는 연결 리스트로 구현할 수 있다.

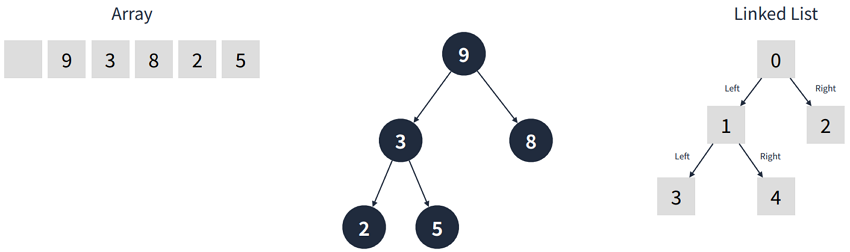
Data Structure_9_4

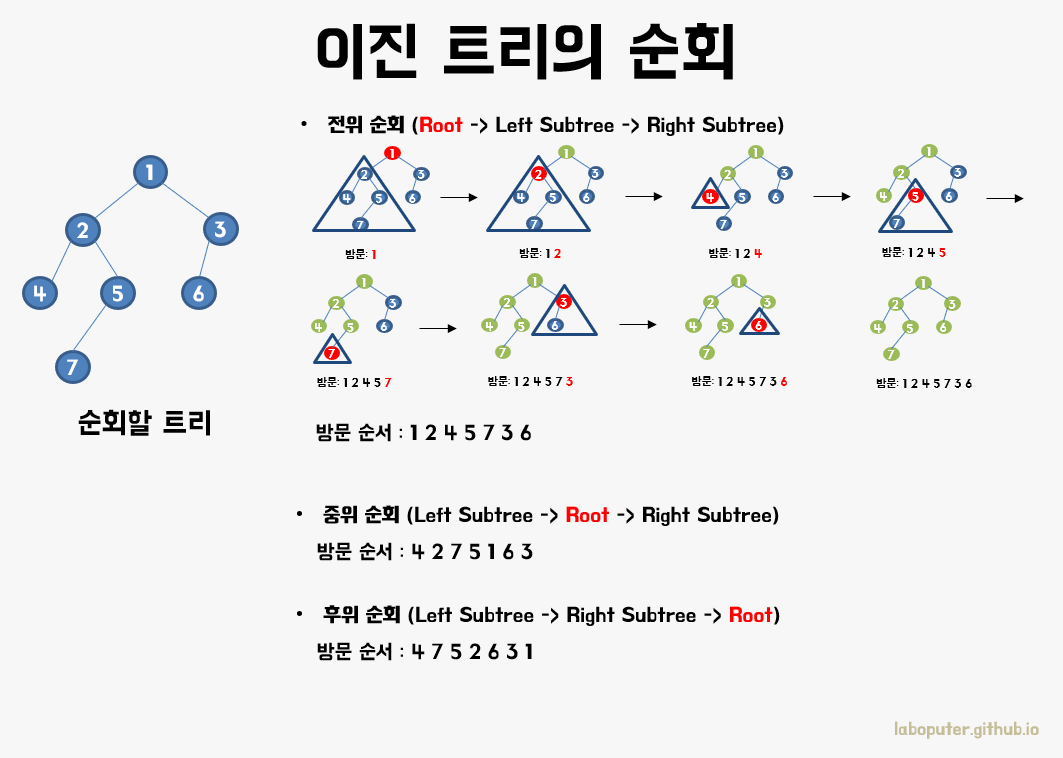
2.3 이진 트리의 순회

Data Structure_9_5

전위 순회(Preorder Traversal): (루트) -> 왼쪽 서브트리 -> 오른쪽 서브트리
중위 순회(Inorder Traversal): 왼쪽 서브트리 -> (루트) -> 오른쪽 서브트리
후위 순회(Postorder Traversal): 왼쪽 서브트리 -> 오른쪽 서브트리 -> (루트)

2. 구현

2.1 이진 트리(Array)

1// 0번 인덱스는 편의를 위해 비워둔다.
2// Left 정점 = Index * 2
3// Right 정점 = Index * 2 + 1
4// Parent 정점 = floor(Index / 2)
5const tree = [
6  undefined,
7  // 1
8  9,
9  // 1*2, 1*2+1
10  3,
11  8,
12  // 2*2, 2*2+1, 3*2, 3*2+1
13  2,
14  5,
15  undefined,
16  7,
17  // 4*2, 4*2+1, 5*2, 5*2+1
18  undefined,
19  undefined,
20  undefined,
21  4,
22]

2.2 이진 트리(Linked List)

1class Node {
2  constructor(value) {
3    this.value = value
4    this.left = null
5    this.right = null
6  }
7}
8
9class Tree {
10  constructor(node) {
11    this.root = node
12  }
13  display() {
14    // Level Order
15    const queue = new Queue()
16    queue.enqueue(this.root)
17    while (queue.size) {
18      const currentNode = queue.dequeue()
19      console.log(currentNode.value)
20      if (currentNode.left) queue.enqueue(currentNode.left)
21      if (currentNode.right) queue.enqueue(currentNode.right)
22    }
23  }
24}
25
26const tree = new Tree(new Node(9))
27tree.root.left = new Node(3)
28tree.root.right = new Node(8)
29tree.root.left.left = new Node(2)
30tree.root.left.right = new Node(5)
31tree.root.right.right = new Node(7)
32tree.root.left.right.right = new Node(4)

[참고]

08-graph(그래프)10-heap(힙)