1. 선형 탐색

정리가 안된 책장에서 원하는 책을 찾는 방법은? 사람마다 다르겠지만 어느 방향이든 처음부터 순차적으로 찾을 수 있습니다.

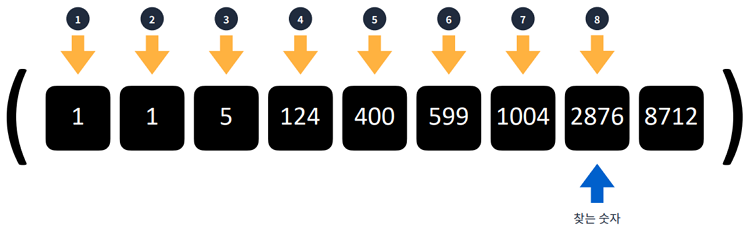
Data Structure_12_1

순서대로 하나씩 찾는 탐색 알고리즘
선형( $O(n)$ ) 시간 복잡도가 걸린다.

2. 이진 탐색

상대방의 나이를 맞추고 싶다면? Up&Down 게임으로 예상 나이를 말하고, 더 큰지 작은지 판단하여 절반씩 줄여나가는 전략을 사용합니다.

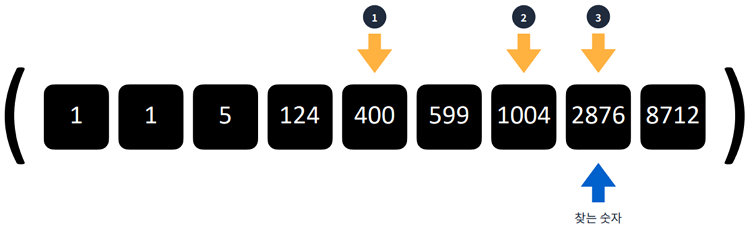
Data Structure_12_2

정렬되어 있는 요소들을 반씩 제외하며 찾는 알고리즘
로그( $O(log\ n)$ ) 시간복잡도가 걸린다.

2.1 이진 탐색의 특징

반드시 정렬되어 있어야 사용가능하다.
배열 혹은 이진 트리를 이용하여 구현할 수 있다.
$O(log\ n)$ 시간복잡도인 만큼 상당히 빠르다.

2.2 배열을 이용한 구현 방법

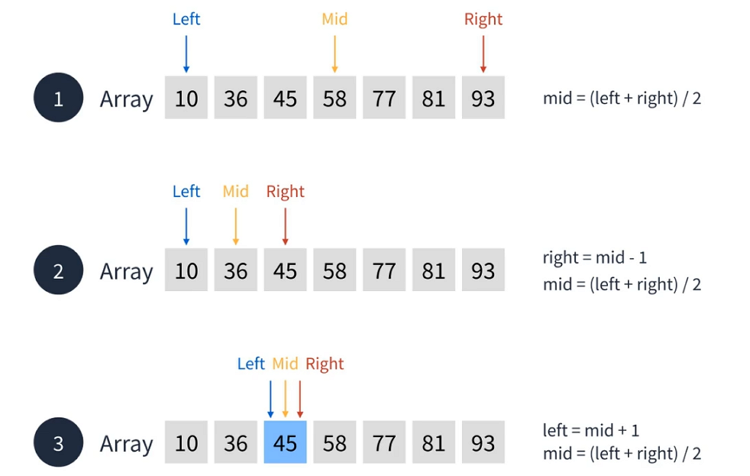
Data Structure_12_3

위 배열에서 45를 찾으려면 어떻게 해야 할까요?

이진 탐색에서는 시작 지점을 Left, 중간을 Mid, 끝 지점을 Right로 둡니다.
- Mid와 찾을 값인 45를 비교합니다
45 < 58 이기 때문에 Right 값을 Mid 1칸 왼쪽에 위치시킵니다.
36 < 45 이기 때문에 Left가 36의 오른쪽으로 이동합니다.
- Left와 Right가 동일하기 때문에 Mid도 동일한 값으로 다시 부여됩니다.
- Mid값과 찾을 값인 45가 같기 때문에 탐색이 종료됩니다.

2.3 이진 탐색 트리를 이용한 구현 방법

배열로 구현하는 방법은 중간에 요소를 추가하거나, 삭제할 떄, 선형시간의 단점을 여전히 들고 있습니다. 그래서 이 방법을 해결하기 위해 이진 탐색 트리를 활용하 수 있습니다.

이진 탐색을 위한 이진트리로 왼쪽 서브 트리는 루트보다 작은 값이 모여있고
오른쪽 서브 트리는 루트보다 큰 값이 모여있다.

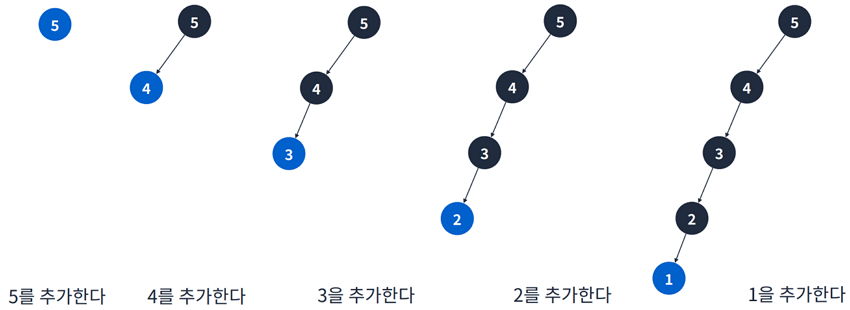
2.3.1 이진 탐색 트리 요소 추가

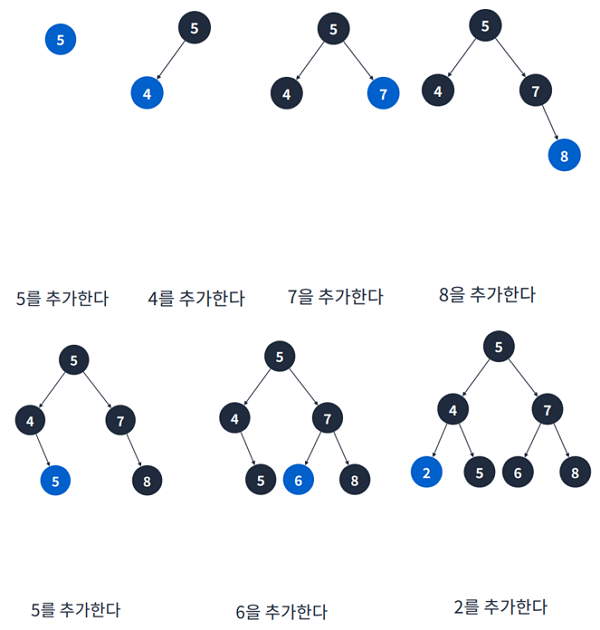
Data Structure_12_4

루트인 5을 추가한다.
4를 추가한다.
- 4 < 5 이기 떄문에 왼쪽 정점에 위치
7을 추가한다.
- 5 < 7이기 때문에 오른쪽 정점에 위치
8을 추가한다.
- 루트인 5 < 8이기 때문에 오른쪽 정점에 위치
- 서브 트리의 루트인 7< 8이기 때문에 오른쪽 정점에 위치
5를 추가한다.
- 동일한 경우 왼쪽, 오른쪽 아무 곳에 넣어도 상관없지만, 여기서는 왼쪽 정점에 넣겠음
- 서브 트리의 루트인 4 < 5이기 때문에 오른쪽 정점에 위치
6을 추가한다.
- 6은 5보다 크고, 7보다 작기 때문에 7의 왼쪽 노드에 추가
2를 추가한다.
- 2는 5보다 작고, 4보다 작기 때문에 4의 왼쪽 노드에 추가

2.3.2 이진 탐색 트리 요소 삭제

(1) 단말 정점을 삭제하는 경우

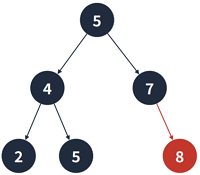
Data Structure_12_5

별다른 처리없이 부모 정점과 연결을 끊으면 된다.

(2) 하나의 서브 트리를 가지는 경우

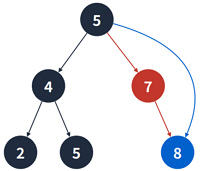
Data Structure_12_6

제거되는 정점의 부모 간선을 자식 정점을 가르키게 바꾸면 된다.

예를 들어, 7을 제거할 경우 5의 오른쪽 간선을 8을 가르키게 하면 된다.

(3) 두 개의 서브 트리를 가지는 경우

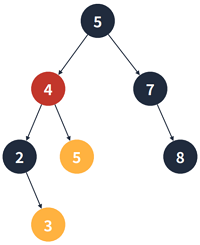
Data Structure_12_7

왼쪽 서브 트리의 가장 큰 값 혹은 오른쪽 서브 트리의 가장 작은 값과 교체하면 된다.
이 경우 교체된 정점의 좌우 자식이 없다면 제거되는 정점의 링크로 대체된다.
- 예를 들어, 4를 삭제할 때, 3 또는 5의 해당하는 정점과 교체하면 됩니다.

2.4 이진 탐색 트리의 문제점

Data Structure_12_8

최악의 경우 한쪽으로 편향된 트리가 될 수 있다.
그런 경우 순차 탐색과 동일한 시간복잡도를 가진다.
이를 해결하기 위해 다음과 같은 자료구조를 이용할 수 있다.
- AVL 트리
- 레드-블랙 트리

3. 이진 탐색 구현

만약 코딩테스트에서 이진 탐색을 사용한다면, 배열을 이용해 구현하는 것을 추천합니다.

3.1 Array

1const array = [1, 1, 5, 124, 400, 599, 1004, 2876, 8712]
2
3function binarySearch(array, findValue) {
4  let left = 0
5  let right = array.length - 1
6  let mid = Math.floor((left + right) / 2)
7
8  // mid가 찾는 값이 일치할 떄까지 순회
9  while (left < right) {
10    if (array[mid] === findValue) {
11      return mid
12    }
13    if (array[mid] < findValue) {
14      left = mid + 1
15    } else {
16      right = mid - 1
17    }
18    mid = Math.floor((left + right) / 2)
19  }
20  // 만약 left값과 right값이 동일할 경우 루프 탈출
21  // 루프를 그대로 빠져나온다면,
22  // 요소를 찾지 못했다는 뜻이기에 - 1반환
23  return -1
24}
25console.log(binarySearch(array, 2876)) // 7
26console.log(binarySearch(array, 1)) // 0
27console.log(binarySearch(array, 500)) // -1

3.2 Binary Search Tree

기존 이진 트리에 탐색 함수를 추가하면 됩니다.

1class Node {
2  constructor(value) {
3    this.value = value
4    this.left = null
5    this.right = null
6  }
7}
8
9class BinarySearchTree {
10  constructor() {
11    this.root = null
12  }
13
14  // 이진 탐색 트리 요소 추가
15  insert(value) {
16    const newNode = new Node(value) // 노드를 하나 생성
17    // 루트가 비어있으면 생성한 노드가 루특가 됨
18    if (this.root === null) {
19      this.root = newNode
20      return
21    }
22
23    let currentNode = this.root
24    // 현재 노드가 null이 아닐 떄까지 순회
25    while (currentNode !== null) {
26      // 만약 오른쪽 노드의 값보다 추가될 노드의 값이 큰 경우 오른쪽 노드에 삽입
27      if (currentNode.value < value) {
28        if (currentNode.right === null) {
29          currentNode.right = newNode
30          break
31        }
32        currentNode = currentNode.right // null이 아닌 경우 이동만 함
33      } else {
34        // 만약 왼쪽 노드의 값보다 추가될 노드의 값이 큰 경우 왼쪽 노드에 삽입
35        if (currentNode.left === null) {
36          currentNode.left = newNode
37          break
38        }
39        currentNode = currentNode.left // null이 아닌 경우 이동만 함
40      }
41    }
42  }
43  has(value) {
44    let currentNode = this.root
45    while (currentNode !== null) {
46      if (currentNode.value === value) {
47        return true
48      }
49      if (currentNode.value < value) {
50        currentNode = currentNode.right
51      } else {
52        currentNode = currentNode.left
53      }
54    }
55    return false
56  }
57}
58
59const tree = new BinarySearchTree()
60tree.insert(5)
61tree.insert(4)
62tree.insert(7)
63tree.insert(8)
64tree.insert(5)
65tree.insert(6)
66tree.insert(2)
67console.log(tree.has(8)) // true
68console.log(tree.has(1)) // false

3. 이진 탐색 실습 : 입국 심사

3.1 문제

https://school.programmers.co.kr/learn/courses/30/lessons/43238

3.2 풀이

1// 로그 시간 = 이진 탐색
2// times -> 선형 로그 시간으로 충분히 가능
3
4// 우리는 특정 값을 찾는 것이 아닙니다.
5// 우리가 찾는 것은 최소 몇 분에 모든 심사가 끝나는가?
6// - 결정 문제 = 이진 탐색 = 파라메트릭 서치(Parametric Search)
7
8// 최소 1분에서 10억분 * n 사이
9// 면접관들이 몇 명을 처리하는가?
10// 처리 가능한 입국자 n보다 작다면, 분을 올려야 하고, 입국자가 n보다 크면 분을 낮춰야 한다.
11// 시간 / 심사시간 = 심사관 당 처리 가능한 입국자 수
12function solution(n, times) {
13  // 오름차순
14  const sortedTimes = times.sort((a, b) => a - b) // O(n log n)
15  let left = 1
16  let right = sortedTimes[sortedTimes.length - 1] * n
17
18  while (left <= right) {
19    const mid = Math.floor((left + right) / 2)
20    // sum([시간 / 심사시간])
21    const sum = times.reduce((acc, time) => acc + Math.floor(mid / time), 0)
22
23    if (sum < n) {
24      left = mid + 1
25    } else {
26      right = mid - 1
27    }
28  }
29  return left
30}

11-trie(트라이)13-sort(정렬)