1. 소수(prime) 구하기

An integer n > 1 is called a prine number, of simply a prime. if its only positive factors are 1 and n. An integer n > 1 that is not a prime is called composite.

1보다 큰 정수들 중, 약수로 1과 자기 자신을 갖는 것을 소수(prime) 그 밖의 수들을 합성수(composite)이라고 한다.

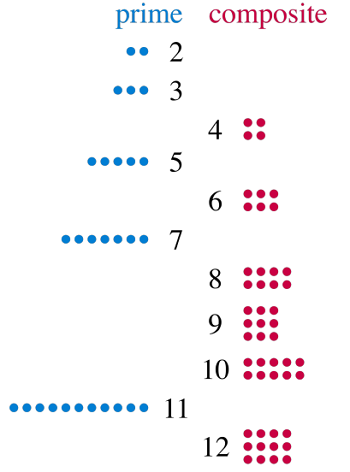
Programmers_JS_Algorithm_16_1

소수는 1 또는 자기 자신만은 약수로 가지는 수를 의미한다.

2. 소수를 구하는 효율적인 방법

2.1 가장 직관적인 방법

2부터 N-1까지 루프를 돌며 나눠보기

Programmers_JS_Algorithm_16_2

다른 방법들에 비해 느린 편에 속한다.

1// O(n)
2function is_prime(num) {
3  for (let i = 2; i < num; i += 1) {
4    if (num % i == 0) {
5      return false
6    }
7  }
8  return true
9}

2.2 효율성 개선하기

그 어떤 소수도 N의 제곱근보다 큰 수로 나눠지지 않는다는 점을 이용

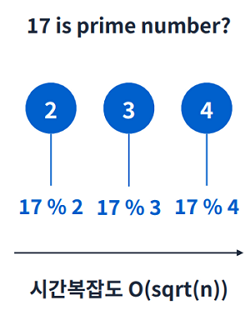
Programmers_JS_Algorithm_16_3

이전 방법보다 더 효율적이다.

1// O(루트 n)
2function is_prime(num) {
3  for (let i = 2; i * i <= num; i += 1) {
4    if (num % i == 0) {
5      return false
6    }
7  }
8  return true
9}

2.3 에라토스테네스의 체⭐

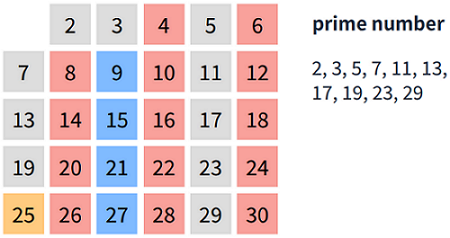
Programmers_JS_Algorithm_16_4

고대 그리스 수학자 에라토스테네스가 발견한 소수를 찾는 방법으로 소수를 판단할 떄, 가장 효율적인 알고리즘

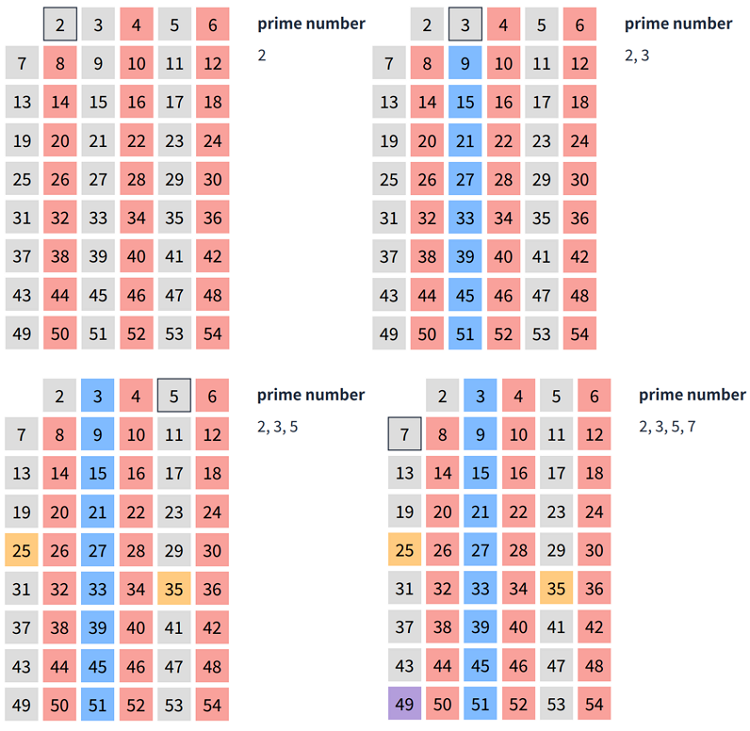
2를 제외한 2의 배수가 되는 수들을 모두 체크
3의 배수가 되는 수들을 모두 체크
4는 이미 체크되어 있기 떄문에 넘어감
5의 배수가 되는 수들을 모두 체크
7의 배수가 되는 수들을 모두 체크

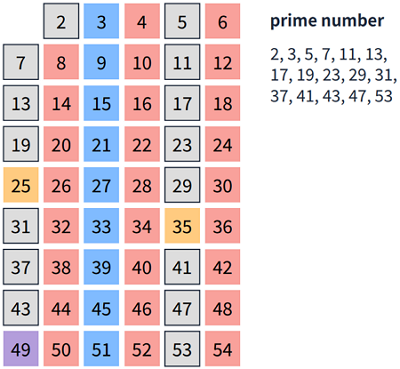
Programmers_JS_Algorithm_16_6

8부터는 확인할 필요가 없다
이후 54까지 체크되지 않은 수들은 모두 소수로 판단

에라토스테네스의 체는 1부터 N까지 모든 소수를 구하는 경우 가장 효율적이다.

1// 에라토스테네스의 체
2// O(n log log n)
3function get_primes(num) {
4  // 0과 1을 제외한 입력값의 나머지 숫자까지 true를 담은 배열
5  const prime = [false, false, ...Array(num - 1).fill(true)]
6
7  // 2 ~ 입력받은 수까지 순회
8  for (let i = 2; i * i <= num; i += 1) {
9    // 2, 3, 4 순으로 배수들을 false로 체크
10    if (prime[i]) {
11      for (let j = i * 2; j <= num; j += i) {
12        prime[j] = false
13      }
14    }
15  }
16  return prime.filter(Boolean) // false같은 값을 제거
17}

2.3.1 추가 설명 : filter(Boolean)

1const something = [...some].filter(Boolean)

왜 이렇게 사용할까? JS에서 제공되는 배열은 아래와 같이 선언하여 사용할 수 있다.

1const bad = undefined
2const bomb = [undefined, 5, null, , , undefined]
3
4const arr = [bad, 1, 2, ...bomb]
5// arr = [undefined, 1, 2, undefined, 5, null, undefined, undefined, undefined]

위에서 제공되는 예시와 같이 undefined 또는 null이 의도하지 않게 들어갈 수 있다. 이러한 가능성은 반복문에서 문제가 발생될 가능성이 크다.

1arr.map(item => {
2  console.log(item.value) // ERROR! Uncaught TypeError: Cannot read property 'item' of undefined
3})

이를 해결하기위해 일반적으로 반복문 내에서 체크하는 로직을 삽입하여 처리하기도 한다.

1arr.map(item => {
2  if (item) {
3    return item
4  }
5
6  console.log(item.value)
7})

하지만 이러한 처리방식은 두가지의 문제점을 야기한다.

코드가 복잡해진다.
배열이 또다른 새로운 배열로 확장되는 경우 또는 배열이 재사용되는 경우 동일하게 체크하는 로직을 삽입하여야한다.

이보다 더 좋은 방법은 없을까? 그 방법이 filter(Boolean)을 사용하여 배열을 믿을 수 있는 상태로 만드는 것이다! 심플하고 간단하게 사용할 수 있다.

1let array = [false, 0, -0, 0n, '', null, undefined, NaN, { hello: 'world' }]
2
3console.log(array.filter(Boolean)) // [{hello: "world"}]

Boolean을 iterator 로 사용하여 false, 0, -0, 0n, "", null, undefined, NaN를 제거할 수 있다.

Reference : https://michaeluloth.com/filter-b

3. 실습 : 소수 찾기

3.1 문제

1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요. 소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다. (1은 소수가 아닙니다.)

[제한 조건]

n은 2이상 1000000이하의 자연수입니다.

[입출력 예]

n	result
10	4
5	3

3.2 풀이

이 문제는 이름 그대로 1부터 입력받은 숫자 n 사이에 있는 소수를 찾는 문제입니다. 1부터 n까지 소수를 모두 찾아야할 경우 가장 효율적인 알고리즘은 에라토스테네스의 체라고 말씀드린 것 기억나시나요? 이번 문제는 에라토스테네스의 체를 이용하여 쉽게 풀 수 있습니다.

그렇지만 다른 알고리즘도 이용하여 한 번 비교해보도록 하겠습니다.

3.2.1 단순 루프로 풀어보기

단순히 2부터 N까지 루프를 도는 것으로 일단 풀어볼 수 있습니다. 코드는 다음과 같습니다.

1// O(n)
2function isPrime(num) {
3  for (let i = 2; i < num; i += 1) {
4    if (num % i == 0) {
5      return false
6    }
7  }
8  return true
9}
10
11function solution(n) {
12  let answer = 0
13  for (let i = 2; i <= n; i += 1) {
14    if (isPrime(i)) {
15      answer += 1
16    }
17  }
18  return answer
19}

하지만 이 코드의 경우 성능이 느리기 때문에 모든 테스트 케이스를 통과하지 못합니다. 따라서 더 효율적인 방법을 찾아야 합니다.

3.2.2 제곱근 이후 연산하지 않기

영상에서 말씀드린 것처럼 N의 제곱근 이후는 체크할 필요가 없습니다. 따라서 다음과 같이 코드를 개선합니다.

1// O(sqrt(n))
2function isPrime(num) {
3  for (let i = 2; i * i <= num; i += 1) {
4    // 이 부분이 변경됩니다.
5    if (num % i == 0) {
6      return false
7    }
8  }
9  return true
10}
11
12function solution(n) {
13  let answer = 0
14  for (let i = 2; i <= n; i += 1) {
15    if (isPrime(i)) {
16      answer += 1
17    }
18  }
19  return answer
20}

정확성 테스트는 모두 통과하지만 여전히 효율성 테스트는 통과하지 못합니다. 따라서 더 효율적인 알고리즘을 사용해야 합니다.

3.2.3 에라토스테네스의 체

에라토스테네스의 체를 구현한 코드는 다음과 같습니다.

1// 에라토스테네스의 체
2// O(n log log n)
3function get_primes(num) {
4  // 0과 1은 소수가 아니기에 미리 false로 체크합니다.
5  const prime = [false, false, ...Array(num - 1).fill(true)]
6
7  for (let i = 2; i * i <= num; i += 1) {
8    if (prime[i]) {
9      for (let j = i * 2; j <= num; j += i) {
10        prime[j] = false
11      }
12    }
13  }
14  return prime.filter(Boolean) // true만 필터링하고 싶을 경우 이런 방식으로 쓸 수 있습니다.
15}
16
17function solution(n) {
18  return get_primes(n).length
19}

이 경우 효율성 테스트를 통과합니다. 정확도 테스트에서 걸린 시간을 확인해보아도 훨씬 빠르다는 것을 알 수 있습니다.

15-greedy(그리디)17-recursion-call(재귀호출)