1. 자료구조

1.1 자료구조

메모리를 효율적으로 사용하며 빠르고 안정적으로 데이터를 처리하는 것이 궁극적인 목표로 상황에 따라 유용하게 사용될 수 있도록 특정 구조를 이루고 있다.

자주 등장하는 네 가지의 자료구조 = Stack, Queue, Tree, Graph

1.2 전산화

현실에 존재하는 영화 예매를 어떻게 컴퓨터로 옮길 것인가? 무엇을 고려해야 하는가?

현실에서 수행되는 프로세스는?
- 고객은 어떤 영화를 볼 지 고른다.
- 고객은 영화를 예매하기 위해 줄을 선다.
- 고객은 차례가 왔을 떄 좌석을 선택한다.
- 고객은 최종적으로 돈을 지불한다.
소프트웨어에서 어떻게 처리할 것인가?
- 영화를 검색한다. → Trie
- 고객이 많을 경우 줄을 서야한다. → Queue
- 고객은 좌석을 선택할 수 있어야 한다. → HashTable

결국 자료구조는 일차원인 컴퓨터 메모리를 현실에 대응되도록 구조를 만든 것이라 할 수 있다.

1.3 자료구조 종류

단순 구조
- 정수, 실수, 문자열, 트리
선형 구조
- 배열
- 연결리스트
- 스택
- 큐
비선형 구조
- 트리
- 그래프
파일구조
- 순차 파일, 색인파일, 직접 파일

1.3.1 선형 구조

한 원소 뒤에 하나의 원소 만이 존재하는 형태로 자료들이 선형으로 나열되어 있는 구조

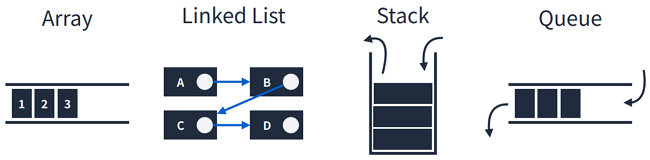
Data Structure_2_1

1.3.2 비선형 구조

원소 간 다대다 관계를 가지는 구조로 계층적 구조나 망형 구조를 표현하기에 적절

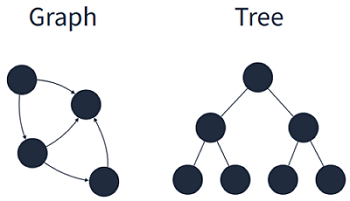
Data Structure_2_2

1.4 완벽한 자료구조는 없다

더 좋고 더 나쁜 자료구조는 없다. 특정 상황에서 유용한 자료구조와 덜 유용한 자료구조가 존재할 뿐이다. 우리는 상황에 맞는 적절한 자료구조를 선택하면 된다.

2. 시간 복잡도

2.1 프로그램의 성능을 정학히 알 수 있는가?

고려할 것

입력 크기
하드웨어 성능
운영체제 성능
컴파일러 최적화
비동기 로직
…

프로그램의 성능을 정학히 파악하는 것은 불가능합니다. 그렇기 때문에 컴퓨터 과학자들은 대략적인 성능을 파악하기 위해 빅오 표기법을 도입했습니다.

시간 복잡도(time complexity)란, 알고리즘의 성능을 나타내는 지표료,

입력 크기에 대한 연산 횟수의 상한을 의미한다.
시간 복잡도는 낮을 수록 좋다.

알고리즘 수행 시간을 측정 방법은 크게 2가지가 있다.

절대 시간을 측정하는 법
1. 프로그램을 작성한 다음에 프로그램을 실행하여 결과가 나올 떄까지의 시간을 측정하면 된다.
2. 이 방법은 프로그램을 실행하는 환경에 따라 달라질 수 있어서 코딩 테스트에서는 잘 활용하지 않는다.
시간 복잡도를 측정하는 법
1. ‘연산 횟수’와 관련이 있다.
2. 즉, 시간 복잡도는 알고리즘이 시작한 순간부터 결과값이 나올 떄까지의 연산횟수를 나타낸다.
3. 시간 복잡도를 측정한 결과는 최선(best), 보통(normal), 최악(worst)의 경우로 나눌 수 있다.

코딩 테스트에서 알고리즘을 성능을 측정할 떄는 2가지가 중요하다.

최악의 경우를 고려하라
- 코테에서는 아주 다양한 조합으로 입력값을 넣어 코드를 평가한다.
- 그 중에는 최악의 입력값도 있을테니, 최악의 경우를 기준으로 시간 복잡도를 분석해야 한다.
알고리즘 성능은 정확히 연산 횟수가 아닌 추이를 활용한다.
- 확인하고 싶은 것은 아주 정확한 연산 횟수가 아니다.
- 내 알고리즘이 제한 시간 안에 수행될 수 있을지 정도를 파악하면 충분하다.
- 따라서 숫자 하나하나 고려해서 구한 정확한 연산 횟수가 아닌, 연산 횟수의 추이를 활용해서 성능을 측정한다.

e.g. 친구와 10시에 만나기로 했는데, 이떄 친구가 ‘언제쯤 도착해?’라고 물었을 떄 1초 단위까지 고민해서 말하지는 않는다.

‘한 5분 전쯤 도착해’라고 말하는게 보통이다.
‘5분 전쯤’안에는 9시 55분 10초, 9시 56분 11초 등 수많은 경우가 있지만, 5분 전쯤이라고 카테고리화할 수 있다.
코테에서도 알고리즘 성능을 측정할 떄도 마찬가지다.
연산 횟수의 추이만 알고 있어도 성능을 충분히 가늠할 수 있고,
- 정확한 연산 횟수를 구할 떄보다 더 빠르다는 장점도 있다.
이런 방식으로 충분히 큰 입력값 N에 따른 연산 횟수의 추이를 활용해,
- 시간 복잡도를 표현하는 방법을 점근적 표기법이라고 한다.
그리고 코테에서는 모든 경우의 수에서 알고리즘 문제를 처리하는 것을 고려해야 하므로,
- 시간 복잡도는 최악의 경우를 가정하여 이야기하는 것이 일반적이다.

2.2 Big-O Notation (빅오 표기법)

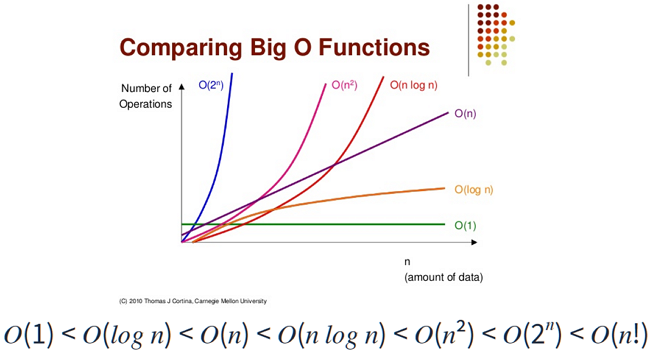
Data Structure_2_3

빅오 표기법은 어떤 프로그램의 연산 횟수가 $f(x)$ 라고 할 떄, 함수의 최고차항을 남기고 계수를 지워 O(...)와 같이 표기하면 된다.

수식	빅오 표기
$f(x) = 2x^2 + 3x + 5$	$O(x^2)$
$f(x) = x + logx$	$O(x)$
$f(x) = 2^x + 10x^5 + 5x^2$	$O(2^x)$
$f(x) = 5x^2 - 6x$	$O(x^2)$

최고차항만 남기고 계수를 지우는 것은 값이 굉장히 커진다면 계수 값들은 의미없을 정도로 작은 값이다.

💡 그럼 빅오 표기법을 어떻게 활용할까?

코딩 테스트 문제에는 제한 시간이 있으므로 문제를 분석한 후에 빅오 표기법을 활용해서 해당 알고리즘을 적용했을 떄, 제한 시간 내에 출력값이 나올 수 있을지 확인해 볼 수 있다.

그러면 문제 조건에 맞지 않는 알고리즘을 적용하느라 낭비하는 시간을 줄일 수 있다.

보통은 다음을 기준으로 알고리즘을 선택한다.

‘컴퓨터가 초당 연산할수 있는 최대 횟수는 1억번이다.’

출제자는 대부분의 코드를 정답 처리하도록 채점 시간을 여유롭게 지정한다.

연산 횟수는 1000~3000만 정도로 고려해서 시간 복잡도를 생각하면 된다.

다음 표를 외울 필요는 없다. ‘이 정도 되는구나’ 감을 잡는 용도로 학습하면 된다.

시간 복잡도 최대 연산 횟수
$O(N!)$ 10
$O(2^N)$ 20 ~ 25
$O(N^3)$ 200 ~ 300
$O(N^2)$ 3,000 ~ 5,000
$O(NlogN)$ 100만
$O(N)$ 1,000 ~ 2,000만
$O(logN)$ 10억

e.g. 1차원 배열은 시간 복잡도가 O(N)으로,

O(N)이 허용하는 연산 횟수는 1,000만이므로 데이터 개수가 1,000만 개 이하면 이 알고리즘을 사용해도 된다.

이렇게 시간 복잡도를 활용해 문제가 제시하는 시간을 초과하는 알고리즘을 제거하면 된다.

시간 복잡도	최대 연산 횟수
$O(N!)$	10
$O(2^N)$	20 ~ 25
$O(N^3)$	200 ~ 300
$O(N^2)$	3,000 ~ 5,000
$O(NlogN)$	100만
$O(N)$	1,000 ~ 2,000만
$O(logN)$	10억

$O(1)$ : 상수 시간❌
- 각 인풋 공간에 변화가 없다.
- 그래서 constant(변함없는) time라 부름
$O(log\ n)$ : 로그 시간
- cf. 로그는 밑이 2
- e.g. 이진 탐색(binary search)
$O(n)$ : 선형 시간(linear time)
- 최악의 경우 n개의 연산을 수행해야 할 경우 적용
- 대부분 간단한 반복문 안에서 constant time연산을 하는 경우
$O(n\ log\ n)$ : 선형 로그 시간
- 실행시간이 입력크기의 로그에 비례
$O(n^2)$ : 2차 시간
$O(2^n)$ : 지수 시간❌
- e.g. 피보나치 수열
$O(n!)$ : 팩토리얼 시간❌

💡 Ref

understanding big O notation with js

엔지니어 대한민국 유튜브 - 빅오표기법 완전정복

2.2.1 $O(n)$ : 선형 시간

1for (let i = 0; i < n; i += 1) {
2  // ...
3}

2.2.2 $O(log\ n)$ : 로그 시간

1for (let i = 0; i <= n; i += 2) {
2  // ...
3}

i = 2n의 값을 볼 수 있으므로 n번째 반복에서는 i = 2n
그러므로 이 결과를 추론할 수 있다.
- $2n < N$
- $log(2n) < log(N)$
- $n < log(N)$

2.2.3 $O(n\ log\ n)$ : 선형 로그 시간

1for (let i = 0; i < n; i += 1) {
2  for (let j = 1; j <= n; i += 2) {
3    // ...
4  }
5}

2.2.4 $O(n^2)$ : 2차 시간

1for (let i = 0; i < n; i += 1) {
2  for (let j = 0; j < n; i += 1) {
3    // ...
4  }
5}

O(n^2+126) = O(n^2) O(3n-30) = O(n) O(3\ log\ n) = O(log\ n)

빅오 표기법은 점근적 표기법을 따릅니다. 점근적 표기법은 함수의 증감 추세를 비교하는 방법입니다.

다음 그림처럼 c와 g가 양수라고 가정하고, n이 $n_0$ 를 넘어설 떄, 함수 $f$ 에는 함수 $g$ 에 한없이 가까워질 순 있지만, 넘을 수는 없습니다. 한마디로, 함수 g(n)에는 함수 f의 한계치라 할 수 있습니다.

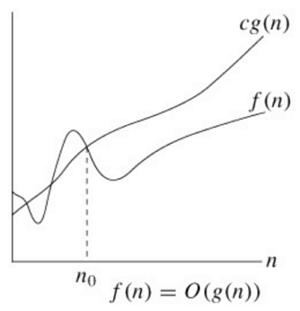
Data Structure_2_4

2.3 빅오표기법 법칙

2.3.1 계수 법칙

상수 $k$ 가 0보다 클 떄 $f(n)=O(g(n))$ 이면 $kf(n)=O(g(n))$ 이다.
$n$ 이 무한에 가까울 수록 $k$ 의 크기는 의미가 없기 떄문이다.

1// 두 루프는 같은 O(n)으로 표기된다.
2for (let i = 0; i < n; i += 1) {
3  // ...
4}
5
6for (let i = 0; i < n * 5; i += 1) {
7  // ...
8}

2.3.2 합의 법칙

$f(n)=O(h(n))$ 이고 $g(n)=O(p(n))$ 이면 $f(n)+g(n)=O(h(n))+O(p(n))$ 이다.
빅오는 더해질 수 있다.

1// 두 루프를 합쳐 O(n + m)으로 표기할 수 있다.
2// 계수 법칙에 의해 5는 사라진다.
3for (let i = 0; i < n; i += 1) {
4  // ...
5}
6
7for (let i = 0; i < m * 5; i += 1) {
8  // ...
9}

2.3.3 곱의 법칙

$f(n)=O(h(n))$ 이고 $g(n)=O(p(n))$ 이면 $f(n)*g(n)=O(h(n))*O(p(n))$ 이다.
빅오는 곱해질 수 있다.

1// 두 루프를 곱해 O(n^2)으로 표기할 수 있다.
2// 계수 법칙에 의해 5는 사라진다.
3for (let i = 0; i < n; i += 1) {
4  for (let j = 0; j < n * 5; j += 1) {
5    // ...
6  }
7}

2.3.4 다항 법칙

$f(n)$ 이 $k$ 차 다항식이면 $f(n)$ 은 $O(n^k)$ 이다.

1// 다음 루프는 O(n^3)으로 표기할 수 있다.
2for (let i = 0; i < n * n * n; i += 1) {
3  // ...
4}

2.3.5 핵심

2가지만 기억하세요.

(1) 상수항은 무시

1// 계수 법칙에 의해 계수는 무시된다.
2// 그리하여 O(n + m)으로 표기된다.
3for (let i = 0; i < n * 6; i += 1) {
4  // ...
5}
6
7for (let i = 0; i < m * 3; i += 1) {
8  // ...
9}

(2) 가장 큰 항 외엔 무시

1// O(n^2 + n)이지만 작은 항은 무시하여
2// O(n^2)으로만 표기해도 된다.
3for (let i = 0; i < n; i += 1) {
4  // ...
5}
6for (let i = 0; i < n; i += 1) {
7  for (let j = 0; j < n; j += 1) {
8    // ...
9  }
10}

2.4 JS에서 성능 측정 방법

2.4.1 Date 객체를 이용

1const start = new Date().getTime()
2
3// ...
4
5const end = new Date().getTime()
6console.log(end - start)

2.4.2 예시

1console.log('start')
2const start = new Date().getTime()
3const N = 1000000000
4
5let total = 0
6for (let i = 0; i < N; i += 1) {
7  total += i
8}
9
10const end = new Date().getTime()
11console.log(end - start)
12console.log('Finish')
13/* 결과
14start
151063
16Finish
17*/

2.5 시간복잡도 계산

2.5.1 별찍기 문제

(1) 문제 정의

숫자 N을 입력받으면 N번째 줄까지 별을 1개부터 N개까지 늘려가며 출력하라는 것

1// N = 3이라면
2*
3**
4***

(2) 연산 횟수를 측정

지금은 출력 자체가 연산이다. 1번 쨰줄은 1번 연산, 2번쨰 줄은 2번 연산, … N번쨰 줄은 N번 연산이다.

(3) 시간 복잡도를 분석

결국 연산 횟수 $f(N)$ 는 다음과 같다. 빅오 표기법으로는 $O(N^2)$ 이라고 할 수 있다.

f(N)=1+2+...+N=\frac{N(N+1)}{2}

2.5.2 박테리아 수명 문제

(1) 문제 정의

초기 박테리아 세포 개수가 N일 떄 해마다 세포 개수가 이전 세포 개수의 반으로 준다면, 언제 모든 박테리아가 죽을지 계산해야 한다.

(2) 연산 횟수를 측정

116 → 8 → 4 → 2 → 1 → 0 (화살표가 5개, 즉 5년)

e.g. N이 16인 경우, 모든 박테리아는 5년이면 소멸한다.

박테리아의 수는 $\left(\frac{1}{2}\right)^Y\cdot N$ 의 값이 최초로 1보다 작아질 떄이다.
수식으로는 $\left(\frac{1}{2}\right)^Y\cdot N\ < 1$ 인 Y를 찾으면 된다.

(3) 시간 복잡도를 분석

이 수식을 다음과 같이 정리할 수 있다.

양변을 N으로 나누면 $\left(\frac{1}{2}\right)^Y < \left(\frac{1}{N}\right)$ 이다.
양변에 역수를 취하고 부등호를 바꾸면 $2^Y > N$ 이다.
양변에 로그를 취하면 $Y > log_2N$ 이다.

이를 통해 이 알고리즘은 $O(logN)$ 의 시간 복잡도를 가진다는 것을 알 수 있다.

3. 자바스크립트 9가지 코드 트릭

3.1 구조 분해 할당을 이용한 변수 swap

ES6의 구조 분해 할당 문법을 사용하여 두 변수를 swap 할 수 있습니다.

1let a = 5
2b = 10
3;[a, b] = [b, a]
4console.log(a, b) // 10 5

3.2 배열 생성으로 루프 제거하기

보통 단순히 범위 루프를 돌고 싶다면 다음과 같이 코드를 작성합니다.

1let sum = 0
2for (let i = 5; i < 10; i += 1) {
3  sum += i // 35 (5~9까지의 합)
4}

만약 범위 루프를 함수형 프로그래밍 방식으로 사용하고 싶다면 배열을 생성해서 사용할 수 있습니다.

1// (_, k) => k + 5
2// _는 보통 사용하지 않는 변수, 파라메터 등에 이름을 붙일 때 사용
3// 특별한 문법적인 기능이 있지는 않지만 관례상 사용되는 규칙
4const sum = Array.from(new Array(5), (_, k) => k + 5) // 5부터 시작하는 유사 배열 생성
5  .reduce((acc, cur) => acc + cur, 0)

💡 from() : 문자열 등 유사 배열(Array-like) 객체나 이터러블한 객체를 배열로 만들어주는 메서드
1Array.from(복사할 배열, 복사하면서 수행할 function)

3.3 배열 내 같은 요소 제거하기

Set을 이용할 수 있습니다.

1const names = ['Lee', 'Kim', 'Park', 'Lee', 'Kim']
2const uniqueNamesWithArrayFrom = Array.from(new Set(names))
3const uniqueNamesWithSpread = [...new Set(names)] // 중복 요소 제거

3.4 Spread 연산자를 이용한 객체 병합

두 객체를 별도 변수에 합쳐줄 수 있습니다.

1const person = {
2  name: 'Lee Sun-Hyoup',
3  familyName: 'Lee',
4  givenName: 'Sun-Hyoup',
5}
6
7const company = {
8  name: 'Cobalt. Inc.',
9  address: 'Seoul',
10}
11
12const leeSunHyoup = { ...person, ...company }
13console.log(leeSunHyoup)
14// {
15//   name: 'Cobalt. Inc.',
16//   familyName: 'Lee',
17//   givenName: 'Sun-Hyoup',
18//   address: 'Seoul' 같은 키는 마지막에 대입된 값으로 정해진다.
19// }

3.5 &&와 || 활용

&&와 ||는 조건문 외에서도 활용될 수 있습니다.

1/// 📝 ||
2// 기본값을 넣어주고 싶을 때 사용할 수 있습니다.
3// participantName이 0, undefined, 빈 문자열, null일 경우 'Guest'로 할당됩니다.
4let participantName,
5  flag = 0
6const name = participantName || 'Guest'
7
8/// 📝 &&
9// flag가 true일 경우에만 실행됩니다.
10flag && func()
11
12// 객체 병합에도 이용할 수 있습니다.
13const makeCompany = (showAddress) => {
14  return {
15    name: 'Cobalt. Inc.',
16    ...(showAddress && { address: 'Seoul' }),
17  }
18}
19console.log(makeCompany(false)) // { name: 'Cobalt. Inc.' }
20console.log(makeCompany(true)) // { name: 'Cobalt. Inc.', address: 'Seoul' }

3.6 구조 분해 할당 사용하기

객체에서 필요한 것만 꺼내 쓰는 것이 좋습니다.

1const person = {
2  name: 'Lee Sun-Hyoup',
3  familyName: 'Lee',
4  givenName: 'Sun-Hyoup',
5  company: 'Cobalt. Inc.',
6  address: 'Seoul',
7}
8
9const { familyName, givenName } = person

3.6.1 객체 생성시 키 생략하기

객체를 생성할 때 프로퍼티 키를 변수 이름으로 생략할 수 있습니다.

1const name = 'Lee Sun-Hyoup'
2const company = 'Cobalt'
3const person = {
4  name,
5  company,
6}
7console.log(person) // { name: 'Lee Sun-Hyoup', company: 'Cobalt' }

3.7 비구조화 할당 사용하기

함수에 객체를 넘길 경우 필요한 것만 꺼내 쓸 수 있습니다.

1const makeCompany = ({ name, address, serviceName }) => {
2  return {
3    name,
4    address,
5    serviceName,
6  }
7}
8const cobalt = makeCompany({
9  name: 'Cobalt. Inc.',
10  address: 'Seoul',
11  serviceName: 'Present',
12})

3.8 동적 속성 이름

ES6에 추가된 기능으로 객체의 키를 동적으로 생성 할 수 있습니다.

1const nameKey = 'name'
2const emailKey = 'email'
3const person = {
4  [nameKey]: 'Lee Sun-Hyoup',
5  [emailKey]: 'kciter@naver.com',
6}
7console.log(person) // { name: 'Lee Sun-Hyoup', email: 'kciter@naver.com' }

3.9 !! 연산자를 사용하여 Boolean 값으로 바꾸기

!! 연산자를 이용하여 0, null, 빈 문자열, undefined, NaN을 false로 그 외에는 true로 변경할 수 있습니다.

1function check(variable) {
2  if (!!variable) {
3    console.log(variable)
4  } else {
5    console.log('잘못된 값')
6  }
7}
8check(null) // 잘못된 값
9check(3.14) // 3.14
10check(undefined) // 잘못된 값
11check(0) // 잘못된 값
12check('Good') // Good
13check('') // 잘못된 값
14check(NaN) // 잘못된 값
15check(5) // 5

01-개요 03-배열과 객체