1. 재귀 함수

재귀 함수는 자기 자신을 호출하는 함수를 말합니다.
- 자기 자신을 호출하는 것을 재귀 호출(Recursion call)이라고 합니다.
함수 호출은 Call Stack에 쌓이기 때문에 스택 자료구조와 유사하게 동작합니다.
함수형 프로그래밍에선 루프 구현을 재귀로 구현하는 경우가 많습니다.
잘못 작성하면 무한 루프에 빠질 수 있습니다.

1.1 JavaScript에서 재귀함수

콜 스택에 제한이 있습니다.
- 자바스크립트 엔진마다 제한 수는 다릅니다.
- 따라서 브라우저마다 다르지만 크롬의 경우 약 1만개 입니다.
꼬리 재귀(Tail recursion)가 제공되지 않습니다.
성능이 좋지 않습니다.

그럼에도 불구하고 재귀를 알아둬야 하는 이유는? 재귀로 작성하면 쉽게 풀리는 코딩 테스트 문제가 있기 떄문! (더 효율적인 것은 아님)

1.2 재귀로 구현해야 편한 알고리즘

불편함을 무시한다면 더 빠른 성능으로 (JS에서) 작성할 수 있지만, 코딩 테스트는 빨리 푸는 것이 중요하기에 추천하지 않는다.

Union-Find
DFS
Backtracking

재귀 함수를 작성할 떄는 반드시 탈출할 수 있는 조건을 작성해야 한다.

1// 재귀 호출
2function recursion(a) {
3  // 탈출 코드가 없으면 무한 루프에 빠진다.
4  return resursion(a + 1) // 자기 자신을 호출하지만 탈출 코드가 없다.
5}

보통 if 문 조건을 통해 탈출한다.

1// 재귀 호출
2function recursion(a) {
3  if (a > 10) {
4    // 무한 루프 방지를 위해 탈출 코드를 작성해야 한다.
5    return a
6  }
7  return recursion(a + 1)
8}
9console.log(recursion(5)) // 11

1.3 피보나치 수열

앞 두 항의 합이 뒤 항의 값이 되는 수열

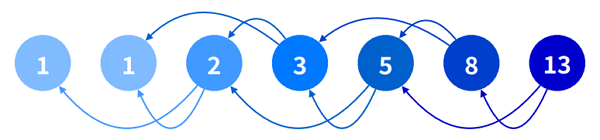
JS_Algorithm_17_1

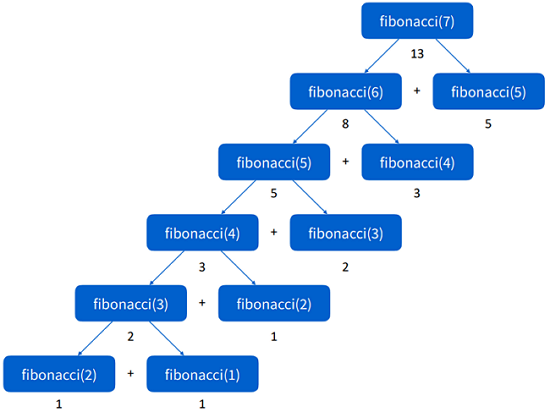
1// 피보나치 수열
2// 1 1 2 3 5 8 13
3function fibonacci(x) {
4  if (x <= 2) {
5    // 무한 루프 방지를 위해 탈출 코드를 작성해야 한다.
6    return 1
7  }
8  return fibonacci(x - 1) + fibonacci(x - 2)
9}
10console.log(fibonacci(7)) // 13

JS_Algorithm_17_2

1.4 변수 없는 합병 정렬(Merge Sort) 구현

합병 정렬이 헷갈린다면 앞 장의 ‘정렬’을 참고하세요.

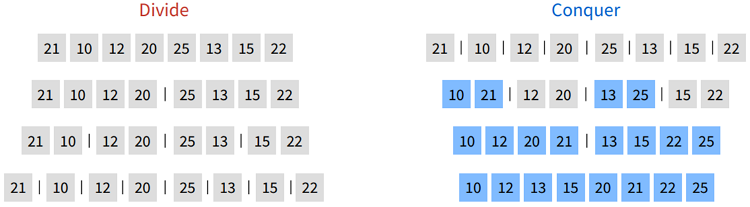
JS_Algorithm_17_3

요소를 나누는 작업부터 먼저 시작합니다. (Divide)
- 8개의 요소를 절반으로 나누고, 요소가 1개가 남을 떄까지 계속 절반으로 나눈다.
모든 요소를 나눴다면 합치는 작업을 시작합니다. (Conquer)
- 나눈 것을 합치면, 두 요소 중 작은 것을 먼저 배치합니다.
- 21과 10의 경우 10이 먼저 배치되고 21이 배치됩니다.
- 이어서 2개까지를 합칠 떄도 작은 순으로 배치합니다.
- 최종적으로 모두 합치면 정렬된 상태가 됩니다.

1// 합병 정렬
2// 결합
3const merge = (a, b) => {
4  if (a.length === 0) return b
5  else if (b.length === 0) return a
6  else if (a[0] < b[0]) return [a[0], ...merge(a.slice(1), b)]
7  else return [b[0], ...merge(a, b.slice(1))]
8}
9
10// 분해
11const mergesort = arr => {
12  if (arr.length < 2) return arr
13  else {
14    const mid = Math.floor(arr.length / 2)
15    return merge(mergesort(arr.slice(0, mid)), mergesort(arr.slice(mid)))
16  }
17}
18console.log(mergesort([21, 10, 12, 20, 25, 13, 15, 22]))
19// [10, 12, 13, 15, 20, 21, 22, 25]

2. 재귀 함수를 이용한 트리 순회

트리 순회는 트리 자료구조에서 각 노드를 한 번씩 탐색하는 알고리즘을 말합니다. 트리 순회에는 여러 방법이 있지만 재귀를 이용할 수 있는 순회는 전위 순회(Preorder), 중위 순회(Inorder), 후위 순회(Postorder)가 있습니다. 모든 순회는 루트 노드부터 시작하며 어떤 노드를 먼저 방문하는지가 달라집니다. 여기서는 이진 트리를 이용하여 설명드리겠습니다.

루트 노드가 앞, 중간, 뒤에 있냐에 따라 전위, 중위, 후위로 나뉜다.

2.1 전위 순회 (Root → Left → Right)

노드를 방문한 후
왼쪽 서브 트리를 전위 순회한 다음
오른쪽 서브 트리를 전위 순회하는 방식

다음과 같은 이진 트리가 있다고 가정 해보겠습니다.

1     1
2    / \
3   /   \
4  2     \
5 / \     3
64   5   / \
7       6   \
8            7
9           / \
10          8   9

1 → 2 → 4 → 5 → 3 → 6 →7 → 8 → 9 노드 순으로 방문

이를 의사 코드로 나타내자면 다음과 같습니다.

1preorder(tree) {
2  방문(tree.root);
3  preorder(tree.left);
4  preorder(tree.right);
5}

2.2 중위 순회 (Left → Root → Right)

왼쪽 서브 트리를 중위 순회한 다음
노드를 방문한 다음
오른쪽 서브 트리를 중위 순회하는 방식

1     1
2    / \
3   /   \
4  2     \
5 / \     3
64   5   / \
7       6   \
8            7
9           / \
10          8   9

4 → 2 → 5 → 1 → 6 → 3 → 8 → 7 → 9 노드 순으로 방문

이를 의사 코드로 나타내자면 다음과 같습니다.

1inorder(tree) {
2  inorder(tree.left);
3  방문(tree.root);
4  inorder(tree.right);
5}

2.3 후위 순회 (Left → Right → Root)

왼쪽 서브 트리를 후위 순회한 다음
오른쪽 서브 트리를 후위 순회한 다음
루트 노드를 방문하는 방식

1     1
2    / \
3   /   \
4  2     \
5 / \     3
64   5   / \
7       6   \
8            7
9           / \
10          8   9

4 → 5 → 2 → 6 → 8 → 9 → 7 → 3 → 1 노드 순으로 방문

이를 의사 코드로 나타내자면 다음과 같습니다.

1postorder(tree) {
2  postorder(tree.left);
3  postorder(tree.right);
4  방문(tree.root);
5}

2.4 구현 코드

이런 전위, 중위, 후위 순회에 대한 재귀 코드 구현은 다음과 같습니다.

1class Node {
2  constructor(value) {
3    this.value = value
4    this.left = null
5    this.right = null
6  }
7}
8
9class Tree {
10  constructor(node) {
11    this.root = node
12  }
13
14  // 전위 순회
15  preorder(currentNode) {
16    console.log(currentNode.value)
17    if (currentNode.left) this.preorder(currentNode.left)
18    if (currentNode.right) this.preorder(currentNode.right)
19  }
20
21  // 중위 순회
22  inorder(currentNode) {
23    if (currentNode.left) this.inorder(currentNode.left)
24    console.log(currentNode.value)
25    if (currentNode.right) this.inorder(currentNode.right)
26  }
27
28  // 후위 순회
29  postorder(currentNode) {
30    if (currentNode.left) this.postorder(currentNode.left)
31    if (currentNode.right) this.postorder(currentNode.right)
32    console.log(currentNode.value)
33  }
34}
35
36const tree = new Tree(new Node(9))
37tree.root.left = new Node(3)
38tree.root.right = new Node(8)
39tree.root.left.left = new Node(2)
40tree.root.left.right = new Node(5)
41tree.root.right.right = new Node(7)
42tree.root.left.right.right = new Node(4)
43
44tree.preorder(tree.root)
45tree.inorder(tree.root)
46tree.postorder(tree.root)

3. 재귀 함수를 이용한 순열, 조합

순열과 조합은 코딩 테스트에서 은근히 자주 사용되는 기능입니다. 아쉽게도 자바스크립트에선 자체적으로 제공하는 built-in 함수가 없기에 직접 구현해야 합니다.

순열과 조합은 재귀 함수를 이용하면 쉽게 만들 수 있습니다. 물론 성능이나 콜 스택 위험으로 인해 스택으로 구현하는 것이 좋지만, 순열과 조합 자체가 시간복잡도가 굉장히 크기 때문에 코딩 테스트에서 n이 크게 나오는 경우는 많지 않습니다. 따라서 재귀로 외우는 것이 직관적이고 편합니다.

3.1 순열

순열의 시간복잡도는 $O(n!)$ 입니다.

1function permutations(arr, n) {
2  // 1개만 뽑는다면 그대로 순열을 반환한다. 탈출 조건으로도 사용된다.
3  if (n === 1) return arr.map(v => [v])
4  let result = []
5
6  // 요소를 순환한다
7  arr.forEach((fixed, idx, arr) => {
8    // 현재 index를 제외한 요소를 추출한다.
9    // index번째는 선택된 요소
10    const rest = arr.filter((_, index) => index !== idx)
11    // 선택된 요소를 제외하고 재귀 호출한다.
12    const perms = permutations(rest, n - 1)
13    // 선택된 요소와 재귀 호출을 통해 구한 순열을 합쳐준다.
14    const combine = perms.map(v => [fixed, ...v])
15    // 결과 값을 추가한다.
16    result.push(...combine)
17  })
18  return result
19}

3.2 조합

조합의 시간복잡도는 $O(2^n)$ 입니다.

1function combinations(arr, n) {
2  // 1개만 뽑는다면 그대로 조합을 반환한다. 탈출 조건으로도 사용된다.
3  if (n === 1) return arr.map(v => [v])
4  const result = []
5
6  // 요소를 순환한다
7  arr.forEach((fixed, idx, arr) => {
8    // 현재 index 이후 요소를 추출한다.
9    // index번째는 선택된 요소
10    const rest = arr.slice(idx + 1)
11    // 선택된 요소 이전 요소들을 제외하고 재귀 호출한다.
12    const combis = combinations(rest, n - 1)
13    // 선택된 요소와 재귀 호출을 통해 구한 조합을 합쳐준다.
14    const combine = combis.map(v => [fixed, ...v])
15    // 결과 값을 추가한다.
16    result.push(...combine)
17  })
18  return result
19}

3.3 문제 : 두 개 뽑아서 더하기

https://programmers.co.kr/learn/courses/30/lessons/68644?language=javascript

3.3.1 문제풀이

단순히 숫자 중 2개를 뽑은 조합을 구하면 되는 문제입니다. 단, 중복을 제거하고 오름차순으로 정렬하는 것을 잊으면 안됩니다. 위에서 작성한 조합 함수를 이용하면 쉽게 풀 수 있습니다.

1function combinations(arr, n) {
2  if (n === 1) return arr.map(v => [v])
3  const result = []
4
5  arr.forEach((fixed, idx, arr) => {
6    const rest = arr.slice(idx + 1)
7    const combis = combinations(rest, n - 1)
8    const combine = combis.map(v => [fixed, ...v])
9    result.push(...combine)
10  })
11  return result
12}
13
14function solution(numbers) {
15  // 1. 조합을 구한다. n 개중 2개
16  // 2. 조합의 합을 구한다.
17  // 3. 중복을 제거한다.
18  // 4. 오름차순 정렬한다.
19  return [...new Set(combinations(numbers, 2).map(combi => combi[0] + combi[1]))].sort((a, b) => a - b)
20}

3.3.2 풀이 2

1function solution(numbers) {
2  const answer = []
3  for (let i = 0; i < numbers.length; i++) {
4    for (let j = i + 1; j < numbers.length; j++) {
5      answer.push(numbers[i] + numbers[j])
6    }
7  }
8  return [...new Set(answer)].sort((a, b) => a - b)
9}

16-prime(소수)자료구조&알고리즘-py