1. 그래프(Graph)

정점(Node)과 정점 사이를 연결하는 간선(Edge)으로 이루어진 비선형 자료구조
정점 집합과 간선 집합으로 표현할 수 있다.
- e.g. 실생활에서 인물 관계도
- e.g. 지하철 노선도
- e.g. 구글의 페이지 랭크 알고리즘

1.1 그래프의 특징

정점(Node)은 여러 개의 간선을 가질 수 있다.
크게 방향 그래프와 무방향 그래프로 나눌 수 있다.
간선은 가중치를 가질 수 있다.
사이클이 발생할 수 있다.

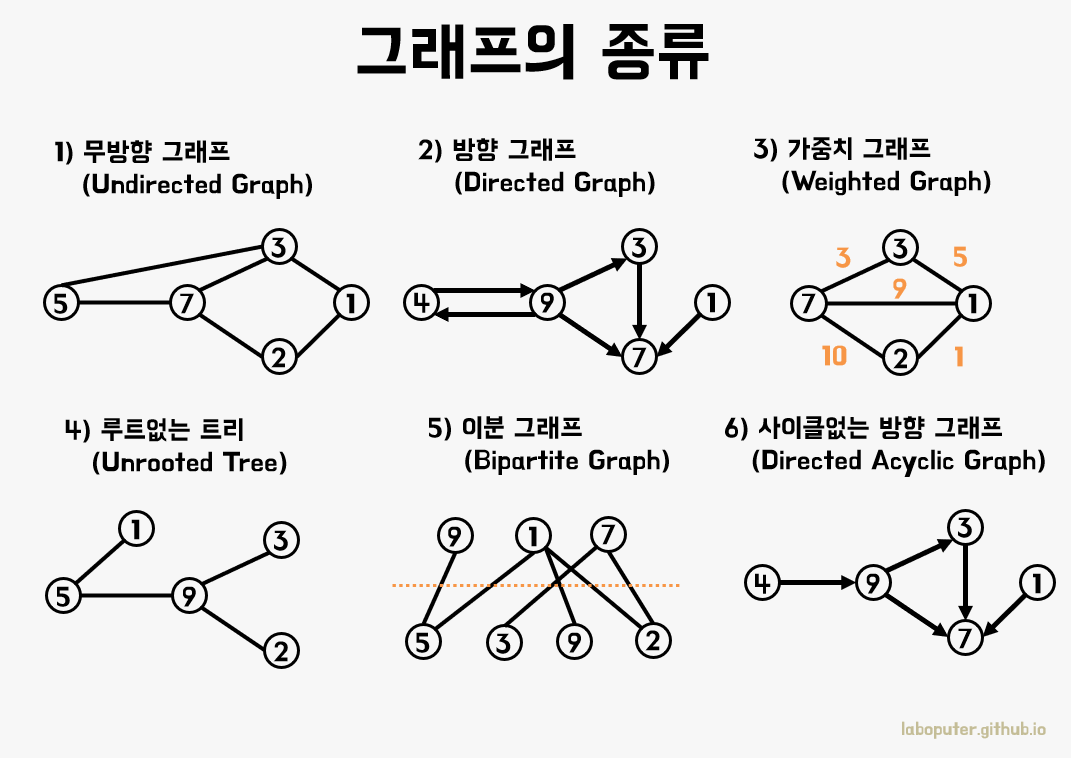
1.2 그래프 종류

Data Structure_8_1

그래프 종류는 간선의 방향, 싸이클 유무에 따라서 나뉠수 있다.

간선 방향에 따른 그래프 종류:

무방향 그래프
방향 그래프
양방향 그래프 (사실상 무방향 그래프 = 양방향 그래프)

싸이클 유무에 따른 그래프 종류:

순환 그래프, 비순환 그래프

방향과 싸이클이 합해지면 다음과 같은 그래프가 나올수 있다.

방향성 비순환 그래프(DAG, Directed Acyclic Graph)
DAG의 실생활 예 - VCS(Version Control System), Cryptocurrency

1.2.1 무방향 그래프

간선으로 이어진 정점끼리는 양방향으로 이동이 가능하다.
표현하기에 (A, B)와 (B, A)는 같은 간선으로 취급된다.
e.g. 양방향 통행 도로

1.2.2 방향 그래프

간선에 방향성이 존재하는 그래프
양방향으로 갈 수 있더라도 <A, B>와 <B, A>는 다른 간선으로 취급된다.
e.g. 일반 통행

1.2.3 연결 그래프

모든 정점이 서로 이동 가능한 상태인 그래프

1.2.4 비연결 그래프

특정 정점쌍 사이에 간선이 존재하지 않는 그래프
e.g. 친한 친구 설문 그래프

1.2.5 완전 그래프

모든 정점끼리 연결된 상태인 그래프

1.2.6 사이클

그래프의 정점과 간선의 부분 집합에서 순환이 되는 부분

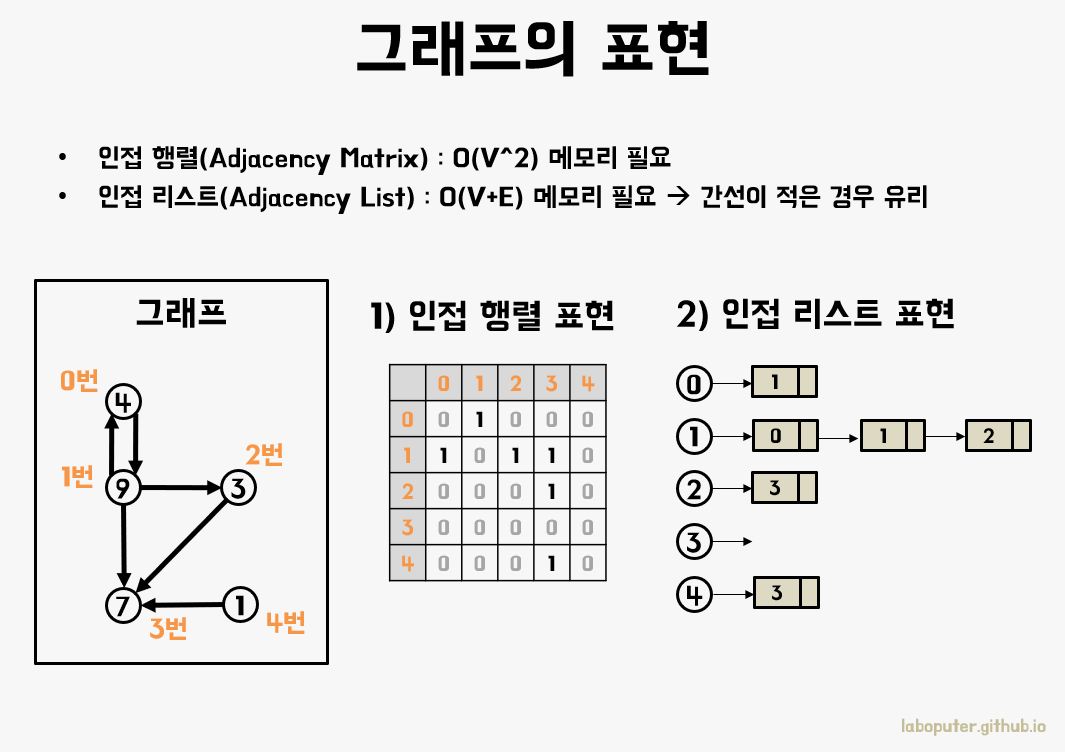
1.8 그래프의 구현 방법

코드로 그래프를 나타내는 방법은 인접 행렬, 인접 리스트 두 가지 방식이 있습니다.

Data Structure_8_2

인접 행렬 : 2차원 배열로 표현이 가능하다.
- 정점 간의 간선의 존재 여부를 1 또는 0로 표현
- 항상 노드 개수의 제곱만큼 메모리( $V^2$ )가 필요한데, 간선이 매우 적으면 비효율적
- 탐색을 할 때도 연결되지 않은 간선들도 확인해야 되기 때문에 느림
인접 리스트 : 연결 리스트로 구현 가능하다.
- 정점 개수만큼 리스트를 만들어 각각의 정점 리스트에 간선 추가
- 메모리도 조금만 사용( $V+E$ )하며 탐색할 때도 연결된 간선만 보면 되기 때문에 빠름

	인접 행렬	인접 리스트
	밀집 그래프를 사용	희소 그래프를 사용
시간 복잡도	$O(v^2)$	$O(V + E) = O(max(V, E))$

그래프에서 간선 개수가 많은 그래프를 밀집(Dense) 그래프라고 한다.
간선 개수가 많지 않은 그래프는 희소(Sparse) 그래프라고 한다.

그래프도 상황에 따라 배열과 리스트 중 무엇으로 구현할 지 선택해야 합니다.

2. 구현

2.1 인접 행렬

1// 정점의 크기만큼 2차원 배열을 만들고, 연결이 안된 상태로 초기화
2const graph = Array.from(Array(5), () => Array(5).fill(false))
3
4// 열 부분을 시작 정점
5// 행 부분을 도착 정점
6// true 값을 넣어주면 연결된 것이라 침
7graph[0][1] = true // 0 -> 1
8graph[0][3] = true // 0 -> 3
9graph[1][2] = true // 1 -> 2
10graph[2][0] = true // 2 -> 0
11graph[2][4] = true // 2 -> 4
12graph[3][2] = true // 3 -> 2
13graph[4][0] = true // 4 -> 0
14
15// 만약 간선에 가중치를 넣고 싶다면, false와 true가 아닌 null과 임의의 가중치값을 넣으면 됩니다.
16// 참고로 무방향 그래프를 구현한다면, 모든 방향을 대칭으로 넣어주면 됩니다.

2.2 인접 리스트

1// 다른 언어와 달리 JS에서 배열은 연결리스트처럼 무한정 늘어나기 때문에
2// 정점의 수 만큼 배열을 만들고, 연결할 정점을 배열에 추가하면 됩니다.
3const graph = Array.from(Array(5), () => [])
4
5graph[0].push(1) // 0 -> 1
6graph[0].push(3) // 0 -> 3
7graph[1].push(2) // 1 -> 2
8graph[2].push(0) // 2 -> 0
9graph[2].push(4) // 2 -> 4
10graph[3].push(2) // 3 -> 2
11graph[4].push(0) // 4 -> 0

3. BFS, DFS 실습 : 가장 먼 노드❌

3.1 문제

https://school.programmers.co.kr/learn/courses/30/lessons/49189

3.2 풀이

1// 핵심 키워드는 '노드', '간선', '최단경로'
2// 최단 경로가 제일 큰 경우의 집합을 구하는 문제
3function solution(n, edge) {
4  const graph = Array.from(Array(n + 1), () => []) // 그래프를 담을 빈 배열
5  console.log(graph)
6
7  // 간선들을 순회
8  for (const [src, dest] of edge) {
9    // 양방향이기 때문에 둘 다 갈 수 있도록
10    graph[src].push(dest) // 원점에서 출발지를
11    graph[dest].push(src) // 출발지에서 원점으로
12  }
13
14  // 각 정점의 길이를 알 수 있도록 하는 0으로 초기화된 배열 생성
15  const distance = Array(n + 1).fill(0)
16  distance[1] = 1
17
18  // BFS : 큐를 이용해 구현 가능
19  const queue = [1]
20  while (queue.length > 0) {
21    // shift는 O(n)이지만 요소가 적을 경우에는 자바스크립트 엔진에서 최적화를 해줌
22    const src = queue.shift()
23    for (const dest of graph[src]) {
24      if (distance[dest] === 0) {
25        queue.push(dest)
26        distance[dest] = distance[src] + 1
27      }
28    }
29  }
30
31  const max = Math.max(...distance) // 최대값
32  return distance.filter(item => item === max).length
33}
34
35console.log(
36  solution(6, [
37    [3, 6],
38    [4, 3],
39    [3, 2],
40    [1, 3],
41    [1, 2],
42    [2, 4],
43    [5, 2],
44  ]),
45)

예를 들어 첫 인자가 [3,6]이 들어온다고 가정했을 때 graph[3].push(6)을 해석해보면, 3번째 graph 배열에 6을 푸시한다. 라고 알 수 있습니다!

1for (const [src, dest] of edge) {
2  graph[src].push(dest)
3  graph[dest].push(src)
4}

이 부분은 양방향 그래프를 만들어주기 위함입니다. 리스트를 이용하여 인접 리스트 형태로 그래프를 만든 것이라 볼 수 있습니다. :) 예를 들어 graph[1]이 [3, 2]라는 값을 담고있다면 1번 정점이 3번과 2번 정점과 연결되어있다라고 볼 수 있습니다. 이 부분을 구체적으로 풀어보면 다음과 같습니다.

1[
2[],
3[ 3, 2 ],         // 1번 정점이 3번과 2번 정점과 연결되어 있습니다.
4[ 3, 1, 4, 5 ],   // 2번 정점이 3번, 1번, 4번, 5번 정점과 연결되어 있습니다.
5[ 6, 4, 2, 1 ],   // 3번 정점이 6번, 4번, 2번, 1번 정점과 연결되어 있습니다.
6[ 3, 2 ],         // 4번 정점이 3번, 2번 정점과 연결되어 있습니다.
7[ 2 ],            // 5번 정점이 2번 정점과 연결되어 있습니다.
8[ 3 ]             // 6번 정점이 3번 정점과 연결되어 있습니다.
9]

이런 형태로 자료 구조를 만들어 문제를 해결했습니다. :)

3.2.1 큐를 이용한 풀이

1// 핵심 키워드는 '노드', '간선', '최단경로'
2// 최단 경로가 제일 큰 경우의 집합을 구하는 문제
3
4// 큐 구현
5class Queue {
6  constructor() {
7    this.queue = []
8    this.front = 0
9    this.rear = 0
10  }
11  enqueue(value) {
12    this.queue[this.rear++] = value
13  }
14  dequeue() {
15    const value = this.queue[this.front]
16    delete this.queue[this.front]
17    this.front += 1
18    return value
19  }
20  isEmpty() {
21    return this.rear === this.front
22  }
23}
24
25function solution(n, edge) {
26  const graph = Array.from(Array(n + 1), () => [])
27
28  for (const [src, dest] of edge) {
29    graph[src].push(dest)
30    graph[dest].push(src)
31  }
32
33  const distance = Array(n + 1).fill(0)
34  distance[1] = 1
35
36  // BFS : 큐를 이용해 구현 가능
37  const queue = new Queue()
38  queue.enqueue(1)
39  while (!queue.isEmpty()) {
40    // shift는 O(n)이지만 요소가 적을 경우에는 자바스크립트 엔진에서 최적화를 해줌
41    const src = queue.dequeue()
42    for (const dest of graph[src]) {
43      if (distance[dest] === 0) {
44        queue.enqueue(dest)
45        distance[dest] = distance[src] + 1
46      }
47    }
48  }
49
50  const max = Math.max(...distance)
51  return distance.filter(item => item === max).length
52}

[참고]

https://laboputer.github.io/ps/2017/09/29/graph/

07-hash(해시)09-tree(트리)