1. 우선순위 큐

FIFO인 큐와 달리 우선 순위가 높은 요소가 먼저 나가는 큐
우선순위 큐는 자료구조가 아닌 개념이다.
e.g. 줄서기 중에 VIP 고객은 먼저 입장

2. 힙(Heap)

힙은 우선순위 큐를 구현하기 위한 가장 적합한 자료구조입니다.
이진 트리 형태를 가지며,
- 우선순위가 높은 요소가 먼저 나가기 위해 요소가 삽입, 삭제될 때 바로 정렬되는 특징이 있다.
우선순위 큐 != 힙

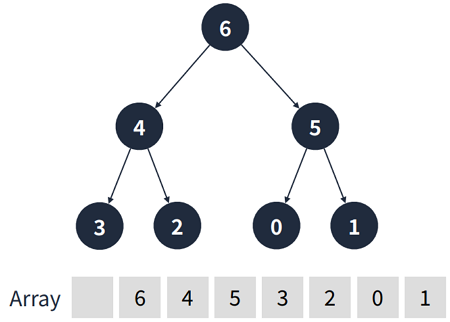
Data Structure_10_1

1.1 힙의 특징

우선순위가 높은 요소가 먼저 나가는 특징을 가진다.
루트가 가장 큰 값이 되는 최대 힙(Max Heap)과 루트가 가장 작은 값이 되는 최소 힙(Min Heap)이 있다.
즉, 빠른 시간 안에 최대값 또는 최소값을 찾아낼 수 있다.
주로 배열을 이용해 힙 구조를 구현할 수 있는데, 다른 언어의 경우 Heap 구조 자체를 라비르러리로 기본 제공한다.
아쉽게도 JavaScript에선 직접 구현해서 사용해야 한다.
물론 코딩테스트 영역 밖이라면 JS 역시 외부 라이브러리를 통해 heap을 사용할 수 있다.

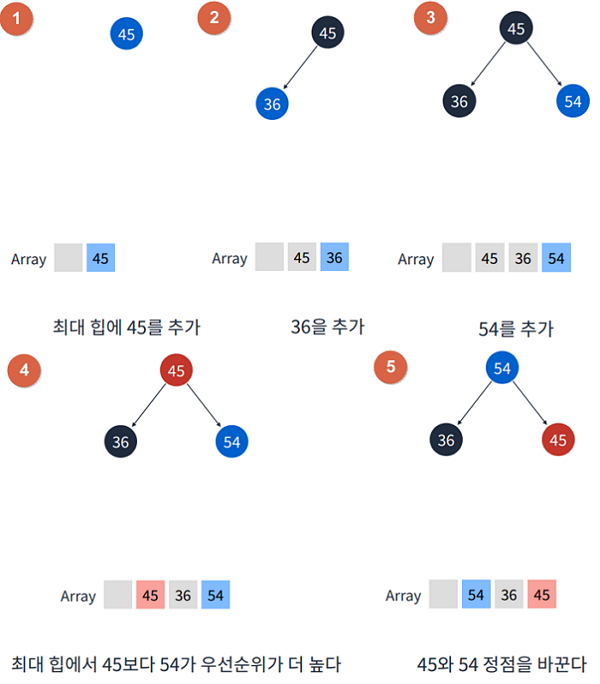
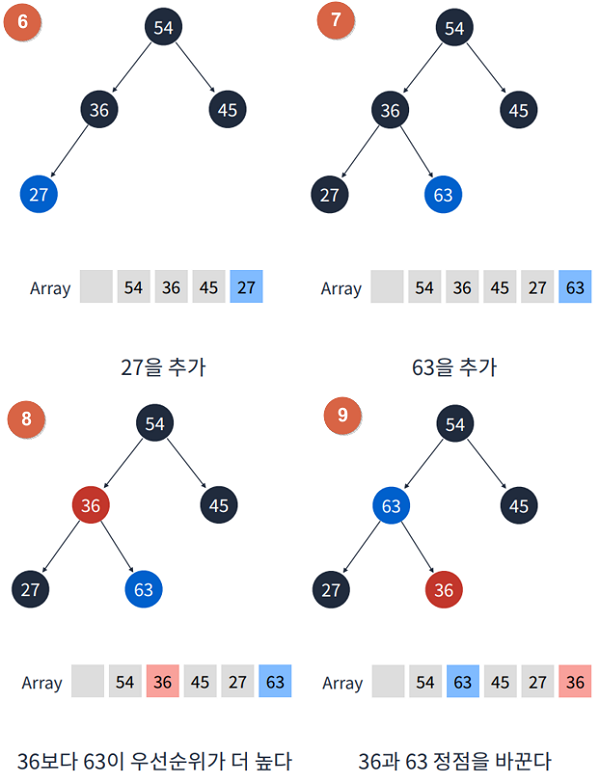
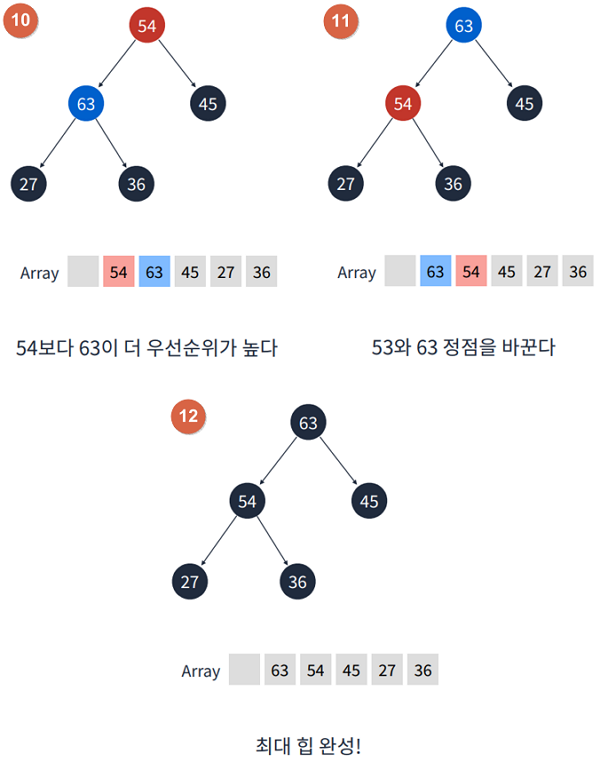
1.2 Heap 요소 추가

요소가 추가될 떄는 트리의 가장 마지막에 정점에 위치한다. - push()
추가 후 부모 정점보다 우선순위가 높다면 부모 정점과 순서를 바꾼다. - swap()
이 과정을 반복하면 결국 가장 우선순위가 높은 정점이 루트가 된다. - heapifyUp()
완전 이진 트리의 높이는 $log\ N$ 이기에 힙의 요소 추가 알고리즘은 $O(log\ n)$ 시간복잡도를 가진다.

Data Structure_10_2

Data Structure_10_3

Data Structure_10_4

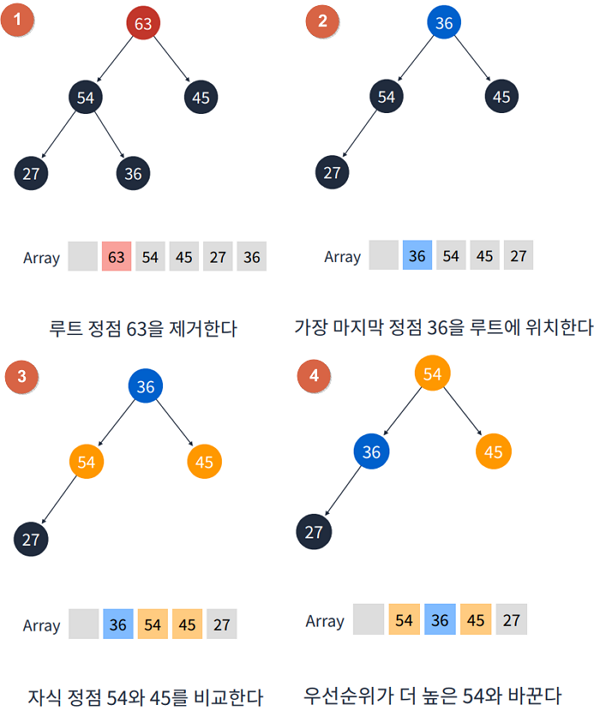
1.3 Heap 요소 제거

요소 제거는 루트 정점만 가능하다.
루트 정점이 제거된 후 가장 마지막 정점이 루트에 위치한다.
루트 정점의 두 자식 정점 중 더 우선순위가 높은 정점과 바꾼다.
두 자식 정점이 우선순위가 더 낮을 때까지 반복한다.
완전 이진 트리의 높이는 $log\ N$ 이기에 힙의 요소 제거 알고리즘은 $O(log\ n)$ 시간복잡도를 가진다.

Data Structure_10_5

Data Structure_10_6

2. 구현

그렇다면 배열을 이용해 어떻게 힙을 구현할 수 있을까? 알고리즘 문제에서 배열의 첫번째 값은 비워두는 경우가 종종 있다. 이는 배열의 첫번째 요소가 가지는 index는 0이기 때문에 ‘1번째’ 라는 말과 인지부조화가 생기기에 계산의 편의성을 위해 그러한 경향을 띄는 편이다. 물론 이러한 부조화에 익숙하다면 굳이 처음을 비워둘 필요는 없지만, 해당 포스팅에서도 역시 계산의 편의성을 위해 첫 배열의 값은 비워두고 시작한다.

1class Heap {
2  constructor() {
3    this.heap = [null] // 첫 원소는 사용 X
4  }
5}

배열의 첫 원소는 사용하지 않으므로 부모와 자식 간 다음의 관계가 성립한다. 완전 이진 트리의 일종이기 때문에 Binaray Search tree에서의 부모-자식 간 관계와 유사하다.

왼쪽 자식의 index = 부모 index * 2
오른쪽 자식의 index = (부모 index * 2) + 1
부모의 index = Math.floor(자식의 인덱스 / 2);

2.1 힙 요소 추가

삽입 역시 비슷하다. 일단 마지막 노드에 들어온 값을 push하여 삽입한다. 이때 재귀적이든 반복문을 돌리든 부모노드를 확인하면서, 들어온 값이 부모노드보다 작은지 큰지를 구분하여 위치를 교환을 계속 실행해주며 정렬해준다. 최대힙으로 구현할 때의 삽입과정을 살펴보자.

최소힙이라면 반대의 계산결과로 적용해주면 된다!

1class MaxHeap {
2  constructor() {
3    this.heap = [null]
4  }
5
6  // 힙 요쇼 추가
7  push(value) {
8    this.heap.push(value)
9    let currentIndex = this.heap.length - 1
10    let parentIndex = Math.floor(currentIndex / 2)
11
12    while (parentIndex !== 0 && this.heap[parentIndex] < value) {
13      const temp = this.heap[parentIndex]
14      this.heap[parentIndex] = value
15      this.heap[currentIndex] = temp
16
17      currentIndex = parentIndex
18      parentIndex = Math.floor(currentIndex / 2)
19    }
20  }
21}
22
23const heap = new MaxHeap()
24heap.push(45)
25heap.push(36)
26heap.push(54)
27heap.push(27)
28heap.push(63)
29console.log(heap.heap) // [ null, 63, 54, 45, 27, 36 ]

2.2 힙 요소 제거

1class MaxHeap {
2  // ...
3
4  // 힙 요소 제거
5  pop() {
6    const returnValue = this.heap[1]
7    this.heap[1] = this.heap.pop()
8
9    let currentIndex = 1
10    let leftIndex = 2
11    let rightIndex = 3
12    while (this.heap[currentIndex] < this.heap[leftIndex] || this.heap[currentIndex] < this.heap[rightIndex]) {
13      if (this.heap[leftIndex] < this.heap[rightIndex]) {
14        const temp = this.heap[currentIndex]
15        this.heap[currentIndex] = this.heap[rightIndex]
16        this.heap[rightIndex] = temp
17        currentIndex = rightIndex
18      } else {
19        const temp = this.heap[currentIndex]
20        this.heap[currentIndex] = this.heap[leftIndex]
21        this.heap[leftIndex] = temp
22        currentIndex = leftIndex
23      }
24      leftIndex = currentIndex * 2
25      rightIndex = currentIndex * 2 + 1
26    }
27    return returnValue
28  }
29}
30
31const heap = new MaxHeap()
32heap.push(45)
33heap.push(36)
34heap.push(54)
35heap.push(27)
36heap.push(63)
37console.log(heap.heap) // [ null, 63, 54, 45, 27, 36 ]
38
39const array = []
40array.push(heap.pop()) // 63
41array.push(heap.pop()) // 54
42array.push(heap.pop()) // 45
43array.push(heap.pop()) // 36
44array.push(heap.pop()) // 27
45console.log(array) // [ 63, 54, 45, 36, 27 ]

3. 힙 실습 : 배상 비용 최소화❌

3.1 문제

OO 조선소에서 태풍으로 인한 작업지연으로 수주한 선박들을 기한 내에 완성하지 못할 것이 예상됩니다. 기한 내에 완성하지 못하면 손해 배상을 해야 하므로 남은 일의 작업량을 숫자로 매기고 배상비용을 최소화하는 방법을 찾으려고 합니다.

배상 비용은 각 선박의 완성까지 남은 일의 작업량을 제곱하여 모두 더한 값이 됩니다.

조선소에서는 1시간 동안 남은 일 중 하나를 골라 작업량 1만큼 처리할 수 있습니다. 조선소에서 작업할 수 있는 N 시간과 **각 일에 대한 작업량이 담긴 배열(works)**이 있을 때, 배상 비용을 최소화한 결과를 반환하는 함수를 만들어 주세요.

예를 들어, N=4일 때, 선박별로 남은 일의 작업량이 works = [4, 3, 3]이라면, 배상 비용을 최소화하기 위해 일을 한 결과는 [2, 2, 2]가 되고 배상 비용은 $2^2 + 2^2 + 2^2 = 12$ 가 되어 12를 반환해 줍니다.

[제한사항]

일할 수 있는 시간 N : 1,000,000 이하의 자연수
배열 works의 크기 : 1,000 이하의 자연수
각 일에 대한 작업량 : 1,000 이하의 자연수

[입출력 예]

N	works	result
4	[4,3,3]	12
2	[3,3,3]	17

[입출력 예 설명]

입출력 예 #1 문제의 예제와 같습니다.

입출력 예 #2 배상 비용을 최소화하기 위해 일을 한 결과는 [2, 2, 3]가 되고 배상 비용은 22 + 22 + 32 = 17가 되어 17를 반환해 줍니다.

3.2 풀이

3.2.1 문제 유형 파악하기

문제 설명 중 핵심 부분은 역시 배상 비용을 계산하는 부분입니다. 배상 비용은 각 요소를 제곱하게 되므로 최대한 각 요소를 골고루 처리하는 것이 가장 배상 비용을 최소화할 수 있는 방법입니다.

그러기 위해서는 매 루프마다 가장 큰 작업을 찾아서 처리해야 합니다. 이때 가장 큰 작업을 찾기 위한 방법은 3가지가 있습니다.

매 루프마다 Math.max 함수를 호출한다.
매 루프마다 정렬한다.
Heap을 이용한다.

1번은 매 루프마다 O(n) 시간복잡도가 소요됩니다. 2번은 O(n log n)이 소요됩니다. 반면 Heap을 이용하면 O(log n)만이 소요됩니다. 사실 매번 큰 값 혹은 작은 값을 알아야 한다면 무조건 Heap을 사용하는 것이 좋습니다. 이제 문제 유형을 파악했으니 한 번 풀어보겠습니다.

3.2.2 최대 힙 구현

가장 큰 값을 알기 위해선 최대 힙을 구현해야 합니다.

1class MaxHeap {
2  constructor() {
3    this.heap = [null]
4  }
5
6  push(value) {
7    this.heap.push(value)
8    let currentIndex = this.heap.length - 1
9    let parentIndex = Math.floor(currentIndex / 2)
10
11    while (parentIndex !== 0 && this.heap[parentIndex] < value) {
12      const temp = this.heap[parentIndex]
13      this.heap[parentIndex] = value
14      this.heap[currentIndex] = temp
15
16      currentIndex = parentIndex
17      parentIndex = Math.floor(currentIndex / 2)
18    }
19  }
20
21  pop() {
22    if (this.heap.length === 2) return this.heap.pop() // 루트 정점만 남은 경우
23
24    const returnValue = this.heap[1]
25    this.heap[1] = this.heap.pop()
26
27    let currentIndex = 1
28    let leftIndex = 2
29    let rightIndex = 3
30    while (this.heap[currentIndex] < this.heap[leftIndex] || this.heap[currentIndex] < this.heap[rightIndex]) {
31      if (this.heap[leftIndex] < this.heap[rightIndex]) {
32        const temp = this.heap[currentIndex]
33        this.heap[currentIndex] = this.heap[rightIndex]
34        this.heap[rightIndex] = temp
35        currentIndex = rightIndex
36      } else {
37        const temp = this.heap[currentIndex]
38        this.heap[currentIndex] = this.heap[leftIndex]
39        this.heap[leftIndex] = temp
40        currentIndex = leftIndex
41      }
42      leftIndex = currentIndex * 2
43      rightIndex = currentIndex * 2 + 1
44    }
45    return returnValue
46  }
47}

3.2.3 solution 함수 구현

빠른 성능으로 통과됩니다.

1function solution(no, works) {
2  // 모든 작업의 합보다 no가 크면 배상 비용을 낼 필요가 없다.
3  if (works.reduce((a, b) => a + b) <= no) {
4    return 0
5  }
6
7  // max heap 구성
8  const heap = new MaxHeap()
9  for (const work of works) {
10    heap.push(work)
11  }
12
13  // no만큼 루프 돌면서 가장 큰 값을 빼서 처리 후 다시 push
14  for (let i = 0; i < no; i += 1) {
15    heap.push(heap.pop() - 1)
16  }
17
18  // 남은 요소에 제곱한 값들의 합을 구한 후 반환
19  return heap.heap.reduce((a, b) => a + b * b)
20}

09-tree(트리)11-trie(트라이)