1. 정렬

만약 구슬들을 크기 별로 나열해야 한다면? 제일 큰 것부터 찾거나 일단 분류해서 정리하는 등의 행동들을 할 것입니다. 이러한 행동을 정렬이라고 부릅니다.

정렬 : 요소들을 일정한 순서대로 열거하는 알고리즘

1.1 정렬의 특징

정렬 기준은 사용자가 정할 수 있다. (e.g. 오름차순, 내림차순)
크게 비교식과 분산식으로 나눌 수 있다.
대부분의 언어가 빌트인으로 제공해준다.
삽입, 선택, 버블, 머지, 힙, 퀵 정렬 등 다양한 정렬 방식이 존재한다.

1.2 어떤 정렬이 제일 빠를까?

정렬들은 각각 유리하고, 불리한 상황이 존재하기 때문에 무엇이 좋고 나쁜지는 정해져 있지 않습니다.

https://www.toptal.com/developers/sorting-algorithms

2. 비교식 정렬

다른 요소와 비교를 통해 정렬을 하는 방식

2.1 버블 정렬(Bubble Sort)

서로 인접한 두 요소를 검사하여 정렬하는 알고리즘
요소들이 마치 거품이 일어나듯이 연쇄적으로 자기 자리를 찾아간다고 해서 버블 정렬이란 이름이 붙여짐
시간복잡도
- Worst Case : $O(n^2)$ - 정렬이 하나도 안되어있는 경우
  - 각 자리를 찾기 위해서 n번의 순회를 해야하며,
  - n번의 회전 동안에 요소의 개수만큼 또 순회를 해야하기 때문
- Best Case : $O(n)$ - 이미 정렬이 되어있는 경우
  - 이미 정렬이 되어있는 경우에는 한 번의 순회로 정렬 여부를 알 수 있다.
즉, 자료의 개수가 많아질수록 성능이 매우 떨어진다
- 5개밖에 없다면 최대 25번 순회하지만, 데이터가 1,000개라면 1,000,000번 순회해야함

2.1.1 동작원리

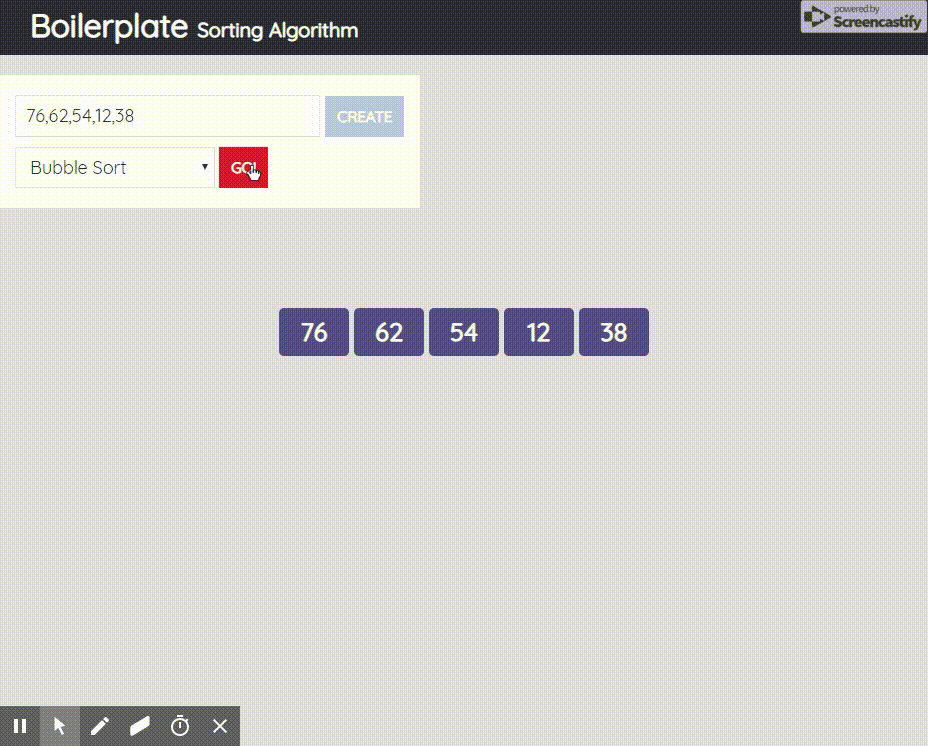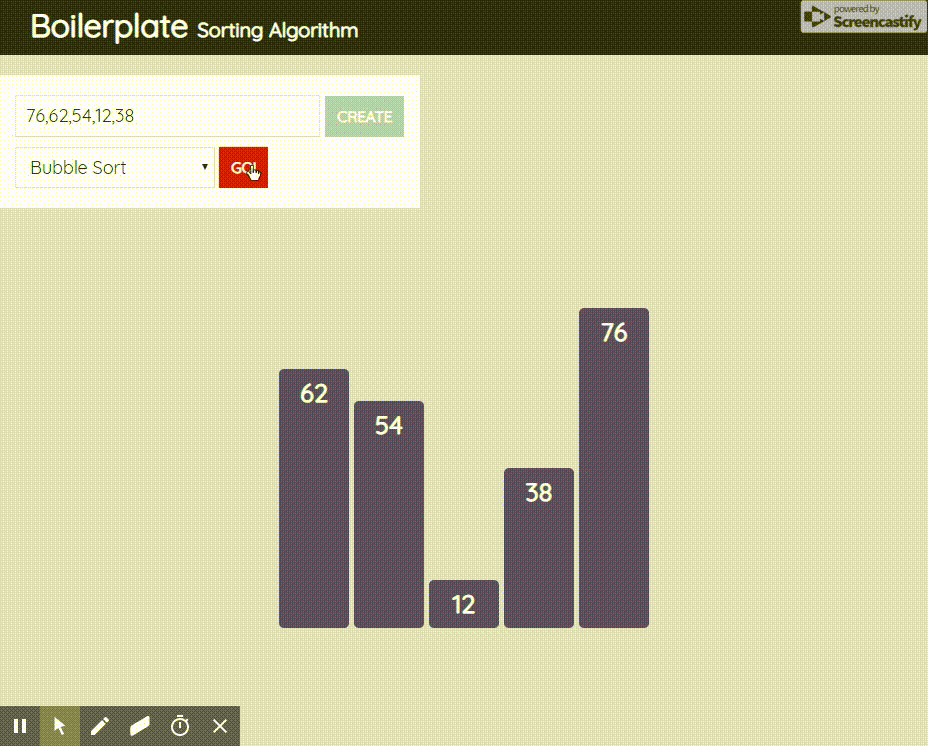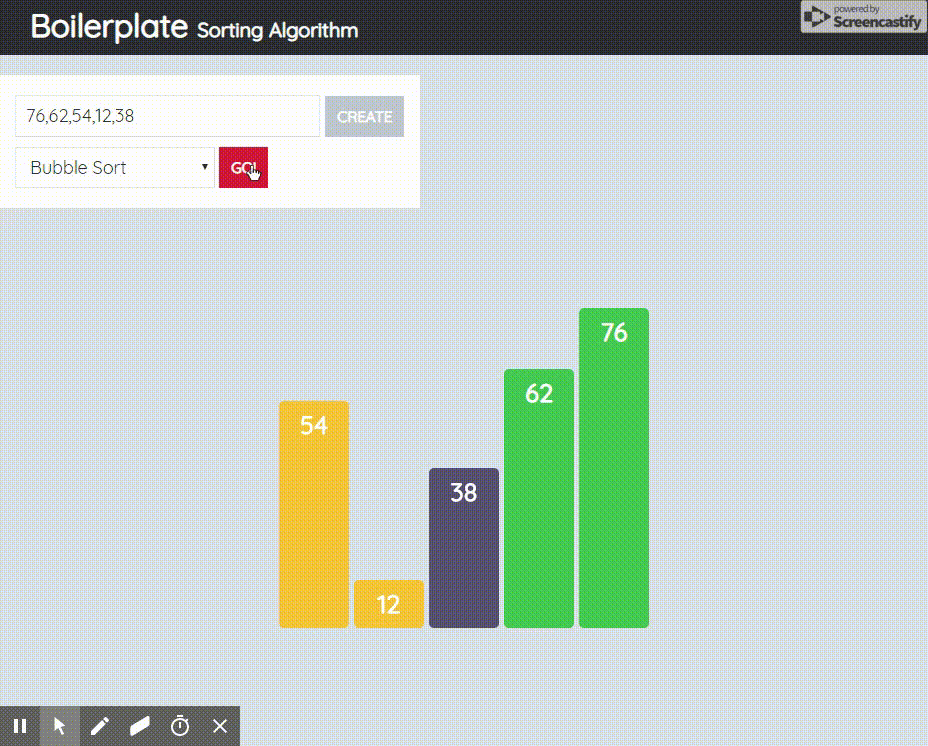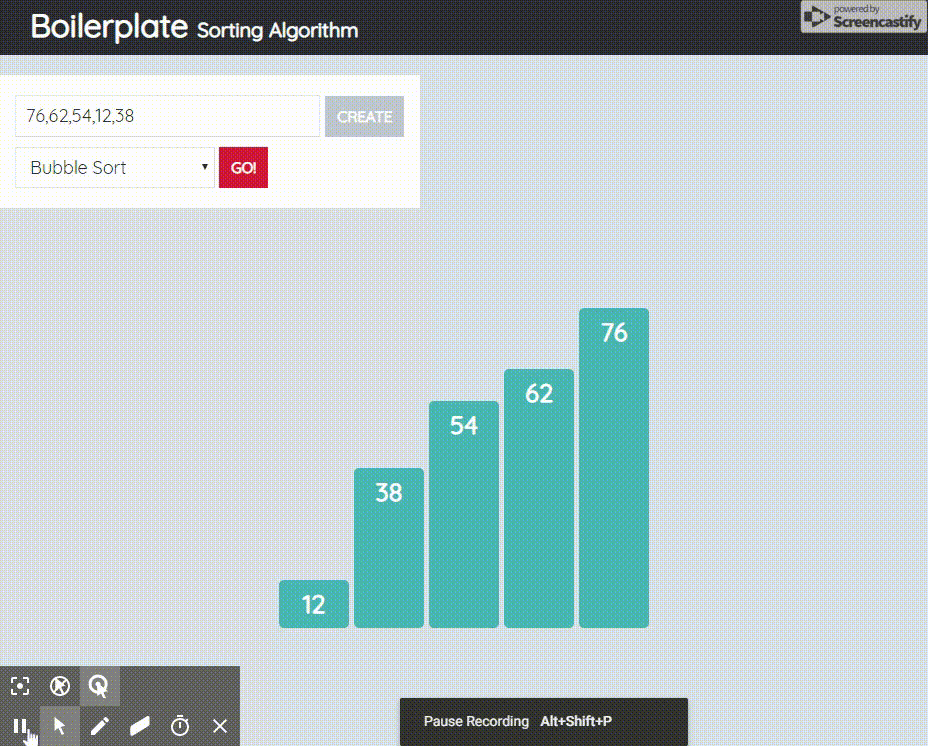
데이터를 두개씩 묶어서 비교한 후 크기가 큰 쪽이 오른쪽으로 가도록 자리를 바꿔가며
크기가 큰 데이터를 오른쪽으로 민다.
그러면 1회전이 끝남과 동시에 이 리스트에서 가장 큰 값이 가장 오른쪽에 가기 때문에 맨 오른쪽 자리가 결정난다.
즉, n번째 정렬 회차가 끝나면 뒤에서 n번째 자리의 데이터가 확정된다.

2.1.2 그림

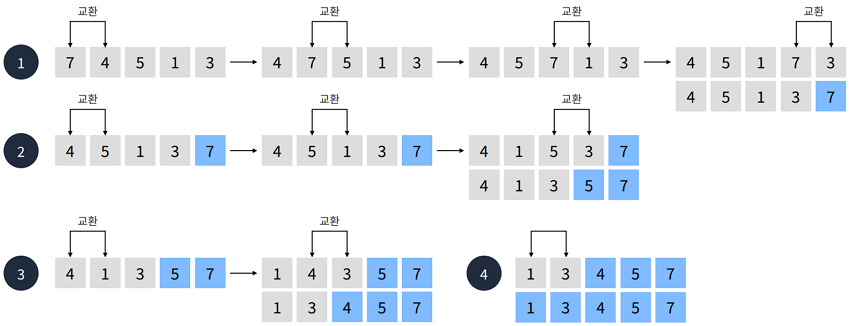
Data Structure_13_1

배열을 오름차순으로 정렬

첫 번쨰 정렬
- 첫 번쨰 요소에 인접한 요소를 비교합니다.
  - 4 < 7 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
- 교환 후 2번쨰 요소와 3번째요소를 비교합니다.
  - 5 < 7 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
- 교환 후 3번쨰 요소와 4번째요소를 비교합니다.
  - 1 < 7 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
- 교환 후 4번쨰 요소와 5번째요소를 비교합니다.
  - 3 < 7 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
두 번째 정렬
- 첫 번쨰 요소에 인접한 요소를 비교합니다.
  - 4 < 5 이기 때문에 교환하지 않습니다.
- 2번쨰 요소와 3번째요소를 비교합니다.
  - 1 < 5 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
- 교환 후 3번쨰 요소와 4번째요소를 비교합니다.
  - 3 < 5 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
세 번째 정렬
- 첫 번쨰 요소에 인접한 요소를 비교합니다.
  - 1 < 4 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
- 2번쨰 요소와 3번째요소를 비교합니다.
  - 3 < 4 이기 때문에 오름차순에 따라 두 요소를 교환합니다.
네 번쨰 정렬
- 첫 번쨰 요소에 인접한 요소를 비교합니다.
  - 1 < 3 이기 때문에 교환하지 않습니다.
- 마무리!

결국 버블 정렬은 n-1번 순회하면 정렬이 마무리됩니다.

2.1.3 구현

1function bubbleSort(arr) {
2  let answer = arr // 얕은 복사
3
4  // 순회
5  for (let i = 0; i < arr.length - 1; i++) {
6    for (let j = 0; j < arr.length - i - 1; j++) {
7      if (arr[j] > arr[j + 1]) {
8        ;[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]] // 바꾸기
9      }
10    }
11    console.log(`${i}회전: ${arr}`)
12  }
13  return answer
14}
15
16console.log(bubbleSort([5, 3, 2, 4, 1]))

2.2 선택 정렬(Selection Sort)

사람이 이해하기 가장 단순한 정렬
선택한 요소와 가장 우선순위가 높은 요소를 교환하는 정렬 알고리즘
시간복잡도
- Worst Case : $O(n^2)$ - 정렬이 하나도 안되어있는 경우
- Best Case : $O(n^2)$ - 이미 정렬이 되어있는 경우
- 정렬이 이미 되어있는 경우에도 $O(n^2)$ 의 시간복잡도를 가짐
- 왜냐하면 매번 정해진 자리에 올 수 있는 최소값을 찾아야하기 때문
- 그래서 성능이 매우 떨어진다.

2.2.1 동작원리

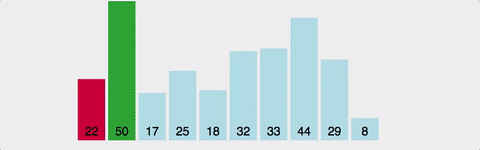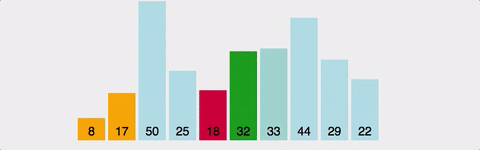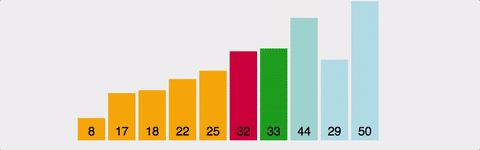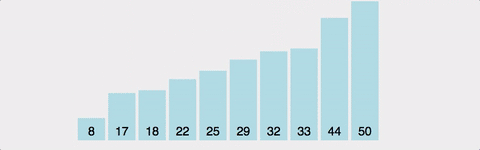
selection-sort

먼저 주어진 리스트 중에 최소값을 찾는다.
그 값을 맨 앞에 위치한 값과 교환한다.
이제 맨 앞을 제외하고 다시 순회하며 최소값을 찾는다.
그 값을 맨 앞 위치 바로 다음 위치와 교체한다. … 반복

버블 정렬이 각 회전이 끝날 때마다 맨 마지막 데이터의 위치가 정해졌던 것과 반대로 선택 정렬은 n번째 회전이 끝날 때마다 앞에서 n번째 데이터의 위치가 정해진다.

2.2.2 그림

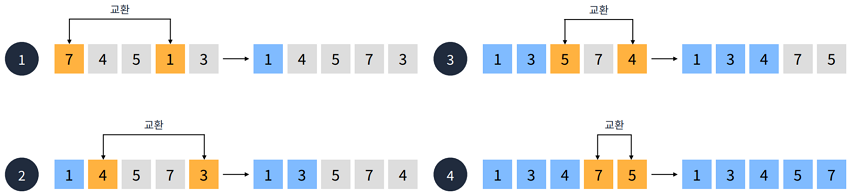
Data Structure_13_2

선택된 첫 번째 요소와 나머지 요소 중 가장 우선순위가 높은 1과 교환합니다.
다음 두 번쨰 요소와 나머지 요소 중 가장 우선순위가 높은 3과 교환합니다.
다음 세 번쨰 요소와 나머지 요소 중 가장 우선순위가 높은 4와 교환합니다.
다음 네 번쨰 요소와 나머지 요소 중 가장 우선순위가 높은 5와 교환합니다.

참고로 나머지 요소 중 선택된 요소보다 우선순위가 높은 요소가 없다면, 교환하지 않고 넘어가면 됩니다.

2.2.3 구현

1function solution(arr) {
2  let answer = arr
3
4  // 크기만큼 순회
5  for (let i = 0; i < arr.length; i++) {
6    let index = i
7
8    for (let j = i + 1; j < arr.length; j++) {
9      if (arr[j] < arr[index]) index = j
10    }
11    ;[arr[i], arr[index]] = [arr[index], arr[i]] // 서로 바꾸기
12    console.log(`${i}회전: ${arr}`)
13  }
14  return answer
15}
16
17console.log(solution([13, 5, 11, 7, 23, 15])) // [ 5, 7, 11, 13, 15, 23 ]

2.3 삽입 정렬(Insertion Sort)

선택한 요소를 삽입할 수 있는 위치를 찾아 삽입하는 방식의 정렬 알고리즘
시간복잡도
- Worst Case : $O(n^2)$ - 정렬이 하나도 안되어있는 경우
- Best Case : $O(n)$ - 이미 정렬이 되어있는 경우
자료의 개수가 많아질수록 성능이 매우 떨어진다

2.3.1 그림

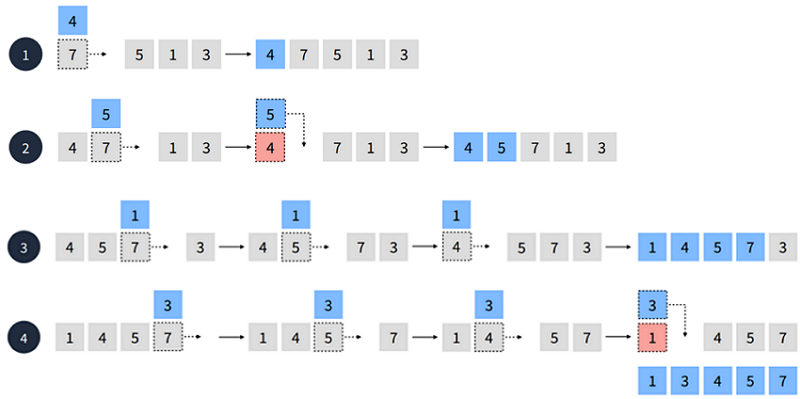
Data Structure_13_3

7, 4, 5, 1, 3순의 배열을 정렬해보겠습니다. 두 번째 요소부터 시작합니다.

두 번째 요소인 4부터 선택합니다.
- 4 < 7 이기 때문에 오름차순에 따라 첫 번쨰 요소에 4을 삽입합니다.
세 번째 요소인 5를 선택합니다.
- 5 < 7 이기 때문에 오름차순에 따라 두 번쨰 요소에 5을 삽입합니다.
- 다음으로 첫 번째 요소와 비교합니다.
- 4 < 5 이기 때문에 오름차순에 따라 밀어내지 못하고 5가 그대로 있습니다.
네 번째 요소인 1를 선택합니다.
- 1 < 7 이기 때문에 오름차순에 따라 세 번쨰 요소에 1을 삽입합니다.
- 1 < 5 이기 때문에 오름차순에 따라 두 번쨰 요소에 1을 삽입합니다.
- 1 < 4 이기 때문에 오름차순에 따라 첫 번쨰 요소에 1을 삽입합니다.
다섯 번째 요소인 3를 선택합니다.
- 3 < 7 이기 때문에 오름차순에 따라 네 번쨰 요소에 3을 삽입합니다.
- 3 < 5 이기 때문에 오름차순에 따라 세 번쨰 요소에 3을 삽입합니다.
- 3 < 4 이기 때문에 오름차순에 따라 두 번쨰 요소에 3을 삽입합니다.
- 1 < 3 이기 때문에 오름차순에 따라 밀어내지 못하고 1이 그대로 있습니다.

2.3.2 구현

1function insertionSort(array) {
2  for (let i = 1; i < array.length; i++) {
3    let cur = array[i]
4    let left = i - 1
5
6    while (left >= 0 && array[left] > cur) {
7      array[left + 1] = array[left]
8      left--
9    }
10    array[left + 1] = cur
11    console.log(`${i}회전: ${array}`)
12  }
13  return array
14}
15console.log(insertionSort([5, 4, 3, 2, 1]))

3. 분산식 정렬

요소를 분산해서 정렬하는 방식

3.1 분할 정복(Divide / Conquer)

Data Structure_13_4

문제를 작은 2개의 문제로 분리하고 더 이상 분리가 불가능할 떄 처리한 후 합치는 전략
정렬 뿐만 아니라 다양한 알고리즘에 응용된다.

3.2 합병 정렬(Merge Sort)

분할 정복 알고리즘을 이용한 최선과 최악이 같은 안정적인 정렬 알고리즘
선형 로그( $O(n\ log\ n)$ ) 시간복잡도를 가진다.

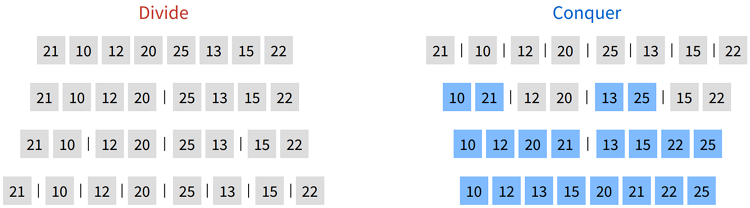
Data Structure_13_5

요소를 나누는 작업부터 먼저 시작합니다. (Divide)
- 8개의 요소를 절반으로 나누고, 요소가 1개가 남을 떄까지 계속 절반으로 나눈다.
모든 요소를 나눴다면 합치는 작업을 시작합니다. (Conquer)
- 나눈 것을 합치면, 두 요소 중 작은 것을 먼저 배치합니다.
- 21과 10의 경우 10이 먼저 배치되고 21이 배치됩니다.
- 이어서 2개까지를 합칠 떄도 작은 순으로 배치합니다.
- 최종적으로 모두 합치면 정렬된 상태가 됩니다.

3.3 퀵 정렬(Quick Sort)

분할 정복 알고리즘을 이용한 매우 빠르지만 최악의 경우가 존재하는 불안정 정렬
선형 로그( $O(n\ log\ n)$ ) 시간복잡도를 가진다.
최악의 경우 2차( $O(n^2)$ ) 시간복잡도를 가진다.

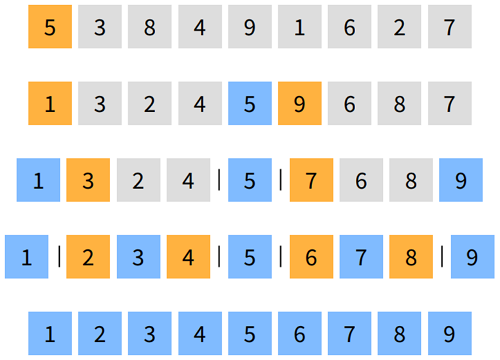
Data Structure_13_6

피벗이라는 기준으로 좌측과 우측을 나눕니다.
- 여기서는 첫 번쨰 요소인 5를 피벗으로 둡니다.
- 5를 기준으로 작은 값이 왼쪽, 큰 값이 오른쪽에 배치됩니다.
다시 나뉜 배열에서 각 첫 번쨰 요소가 피벗이 됩니다.
- 각각 1과 9가 피벗이 됩니다.
다시 나뉜 배열에서 각 첫 번쨰 요소가 피벗이 됩니다.
더 이상 나눌 수 없는 상태가 되었다면, 그대로 합쳐줍니다.

4. JS에서 정렬(sort)

JavaScript에서는 정렬이 매우 간단합니다.

1const array = [5, 9, 10, 3, 8, 3, 2]
2
3// 다음과 같이 그냥 정렬하면 ASCII 문자 순서로 정렬되어
4// 우리가 원하는 숫자 크기대로 정렬되지 않는다.
5array.sort()
6console.log(array) // [10, 2, 3, 3, 5, 8, 9]
7// 10이 먼저 나오는 이유는 ASCII 문자 '1'이 '2'보다 작기 때문
8
9array.sort((a, b) => a - b) // 오름차순 정렬
10console.log(array) // [2, 3, 3, 5, 8, 9, 10]
11
12array.sort((a, b) => b - a) // 내림차순 정렬
13console.log(array) // [10, 9, 8, 5, 3, 3, 2]

[참고]

https://im-developer.tistory.com/133

12-binary-search(이진탐색)14-bfs-dfs